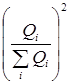Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.

Предыдущая

Оглавление

Следующая

Глава 5. Средние величины

5.4. Показатели дифференциации и концентрации

При изучении вариационного ряда для отражения его структуры, помимо медианы, также применяются другие характеристики. Их общее название – квантили – это порядковые характеристики признака, которые делят все единицы ряда на равные численности. Квантили, по сути, есть варианты, занимающие определенное место (десятое, двадцать пятое, пятидесятое и т.д.) в ранжированной совокупности, в которой в качестве весов используются частости. К числу квантилей, наиболее часто используемых в статистическом анализе, относят перцентили (P), квартили (Q), децили (D) и медиану (Mе).

P-тый перцентиль вариационного ряда – это значение признака, слева от которого лежит P% вариантов ряда. Позиция P-го перцентиля задается как (n+1)P/100, где n-число вариантов ряда. Перцентиль характеризует значение признака в определенной позиции ранжированного ряда, отражает меру относительной позиции варианта в ряду.

Например, по данным выборочного обследования данных о дневной выручке 20 продуктовых магазинов района (тыс.руб) имеем ранжированный ряд следующего вида:

х_i : 9; 9; 11; 12; 15; 16; 17; 18; 19; 21; 21; 25; 25; 26; 26; 26; 26; 27; 30; 30.

Необходимо определить 25-й, 50-й и 90-й перцентили в данном вариационном ряду.

Для определения 25 перцентиля необходимо вначале найти его позицию в вариационном ряду:

(n+1)P/100 = (20+1)25/100 = 5,25.

Эта позиция находится между пятым и шестым значениями признака. Пятое по порядку значение признака ряда равно 15, шестое - 16. Значение перцентиля находится в точке, которая делит расстояние между 15 и 16 в отношении 0,25 к 1, расстояние от 15 до 25-го перцентиля составляет 0,25 от длины отрезка между 15 и 16. Итак, 25-й перцентиль равен 15,25.^[3]

Для того чтобы найти 50 перцентиль, мы должны определить значение варианта, соответствующего позиции :

(n+1)P/100=(20+1)50/100 =10,5.

Просматривая ранжированные значения, мы видим, что 10 значение признака равно 21, а 11-е по порядку значение признака так же равно 21, отсюда, 50-й перцентиль равен 21.

Соответственно, мы определяем 90-й перцентиль как значение варианта, соответствующего позиции (n+1)P/100=(21)90/100=18,9. Отсюда 18 значение признака ряда равно 27, а 19-е равно 30, следовательно, расстояние от 27 до 90-го перцентиля составляет 0,9 от длины отрезка между 27 и 30 (длина отрезка равна трем). Итак, 90-й перцентиль равен 29,7

В статистике часто применяются квантили, которые делят вариационный ряд на четыре равные части - квартили (от латинского слова quarta - четверть): первый квартиль, второй квартиль, третий квартиль и четвертый квартиль (обозначаются Q₁, Q₂, Q₃, Q₄).

Первый квартиль (25-й перцентиль) – это значение признака в вариационном ряду, слева от которого лежит 1/4 (или 25%) всех вариантов. Соответственно, второй квартиль – это 50 перцентиль, он называется  медианой.

Отсюда, медиана – значение признака ряда, относительно которого вариационный ряд делится на две равные по числу вариантов части – это   50-й перцентиль^[4].

Третий квартиль – это точка, слева от которой находится 3/4 или 75% вариантов ряда.

Варианты, отделяющие снизу и сверху в порядке возрастания признака по одной четвертой части совокупности образуют нижний и верхний квартили. 25-й перцентиль называют нижним квартилем, 50-й перцентиль (медиану) – средним квартилем, 75-й перцентиль – верхним квартилем.

В рассматриваемом примере найдены нижний и средний квартили, а верхний квартиль – это точка, соответствующая позиции (21)^.75/100=15,75, его значение равно 26,75.

В статистическом анализе также часто применяют квантили, которые делят вариационный ряд на десять равных частей - децили. В дискретном вариационном ряду их значения определяются, соответственно, как 10, 20, ..., 90 перцентили. Так, позиция первой децили равна: (21)10/100=2,1, следовательно, первая дециль равна 9,1.

Для оценки дифференциации значений признака ряда используются децильный коэффициент дифференциации и коэффициент фондов.

Децильный коэффициент равен отношению девятой децили к первой децили. Он показывает, во сколько раз наименьший уровень признака из 10% единиц, имеющих наибольший уровень признака, больше наибольшего уровня признака, из 10% единиц совокупности, имеющих наименьший уровень признака: К_d = D₉/D₁.

Значит, для рассматриваемого примера децильный коэффициент дифференциации будет равен: K_d = 29,7/9,1 = 3,26. То есть, минимальная выручка в 10% группе наиболее крупных магазинов превышает максимальную выручку в 10% группе небольших магазинов в 2,26 раза.

Коэффициент фондов равен отношению среднего уровня 10-й децили к среднему уровню 1-й децили:

K_f =  = 30/9 = 3,33.

То есть, средняя выручка 10% наиболее крупных магазинов превышает среднюю выручку 10% наиболее мелких магазинов в 3,33 раза.

Государственная статистика регулярно публикует коэффициент фондов для характеристики дифференциации доходов населения (в 2001 году он составлял 14). Однако в исследовательской работе используется и децильный коэффициент дифференциации. Его применение особенно эффективно в тех случаях, когда в распределении доходов в начале первого дециля находятся крайне низкие доходы, а десятый дециль завершается аномально высокими доходами, которые существенно влияют на сумму доходов в этих децилях. В такой ситуации правильнее применять децильный коэффициент дифференциации, а не коэффициент фондов.

Показатели дифференциации охватывают и коэффициенты концентрации. Наиболее известными являются два показателя: коэффициент Джини и коэффициент Герфиндаля.

Коэффициент концентрации Джини рассчитывается по формуле:

,

где p_i – накопленная доля численности единиц ряда; q_i – накопленная доля прибыли, приходящаяся на все единицы ряда с прибылью не более x_i.^[5]

Коэффициент Джини может принимать значения от 0 до 1, чем больше концентрация признака, тем ближе коэффициент Джини к 1.

Коэффициент Герфиндаля вычисляется на основе данных о доле изучаемого признака в j-той группе в совокупном объеме признака. Коэффициент Герфиндаля:

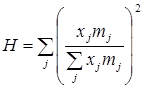 или  ,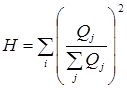

где 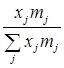  - доля выручки j-той группы в общем объеме выручки всех магазинов;           - объём выручки в j-той группе.

Показатель Н зависит от числа единиц в группах.

Для иллюстрации принципа расчета этих коэффициентов воспользуемся данными нашего примера.

Номера магазинов: i	Значения признака: Выручка магазина: х	Накопленные значения признака: q	Накопленная доля численности единиц  ряда: p	piq i+1	pi+1qi
1	9	9	0,05	0,002	-	0,0005
2	9	18	0,1	0,007	0,002	0,0005
3	11	29	0,15	0,014	0,007	0,0007
4	12	41	0,2	0,025	0,015	0,0009
5	15	56	0,25	0,041	0,027	0,0013
6	16	72	0,3	0,062	0,044	0,0015
7	17	89	0,35	0,087	0,065	0,0017
8	18	107	0,4	0,118	0,092	0,0019
9	19	126	0,45	0,154	0,123	0,0021
10	21	147	0,5	0,198	0,162	0,0026
11	21	168	0,55	0,246	0,205	0,0026
12	25	193	0,6	0,307	0,296	0,0037
13	25	218	0,65	0,373	0,320	0,0037
14	26	244	0,7	0,447	0,388	0,0040
15	26	270	0,75	0,528	0,462	0,0040
16	26	296	0,8	0,615	0,543	0,0040
17	26	322	0,85	0,709	0,630	0,0040
18	27	349	0,9	0,811	0,725	0,0044
19	30	379	0,95	0,927	0,834	0,0054
20	30	409	1,0	-	0,95	0,0054
Итого				5,670	5,584	0,05528

Коэффициент Джини равен 0,18, что свидетельствует о невысоком уровне концентрации выручки магазинов. Значение коэффициента Герфиндаля, равное 0,06, подтверждает этот вывод.

Следует отметить, что приведенные расчеты носят исключительно иллюстративный характер, поскольку экономический смысл этих коэффициентов наиболее полно проявляется лишь при проведении сравнений исследуемых явлений во времени и в пространстве. Например, коэффициент Джини используется для характеристики дифференциации доходов населения в различных регионах РФ или странах, а коэффициент Герфиндаля применяется для характеристики концентрации производства, капитала в различных отраслях, регионах, странах. Основное достоинство коэффициента Герфиндаля – его высокая чувствительность к изменению в суммарном обороте долей крупнейших участников, что позволяет отслеживать концентрацию рыночного оборота и реагирует на число участников рынка.

---

Предыдущая

Оглавление

Следующая