Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 9. Статистическое изучение взаимосвязей
9.2. Статистические методы выявления наличия корреляционной связи между признаками
Простейшим приемом выявления корреляционной связи между двумя признаками является метод параллельного сопоставления рядов. Сущность метода заключается в том, что значения факторного признака располагают в возрастающем порядке и затем прослеживают направление изменения величины результативного признака. В тех случаях, когда возрастание величины факторного признака влечет за собой возрастание и величины результативного признака, можно говорить о возможном наличии прямой корреляционной связи. Если же с увеличением факторного признака результативный имеет тенденцию к уменьшению, то можно предполагать обратную связь между признаками.
Допустим, есть данные о выпуске продукции на 6 однотипных предприятиях (х) и потреблении на них электричества (у). Сравним изменения двух величин и если их вариация согласована, то можно сделать вывод о наличии связи:
|
Выпуск продукции (х) |
5 |
7 |
10 |
12 |
15 |
17 |
|
Потребление электричества (у) |
17 |
22 |
26 |
24 |
30 |
42 |
Таблица наглядно демонстрирует, что с увеличением х возрастает и у, поэтому связь между ними можно считать прямой.
Однако при большом числе различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, параллельные ряды плохо воспринимаются, особенно в больших совокупностях. В подобных случаях для установления факта наличия связи лучше воспользоваться методом группировок.
Метод аналитических группировок. В теме, посвященной сводке и группировке статистических данных, мы уже говорили, что при аналитической группировке исследуется связь между двумя и более признаками, из которых один рассматривается как результат, а другой как фактор (факторных признаков может быть несколько). Для установления связи между признаками данные группируются по признаку-фактору, который располагается в подлежащем аналитической таблицы. Если результативный признак зависит от факторного, то в изменении факторного признака и среднего значения результативного будет обнаруживаться определенная закономерность. Например, связь между продолжительностью оборота оборотных средств и размером прибыли предприятия можно легко обнаружить, сгруппировав предприятия по длительности оборота оборотных средств и рассчитав среднюю прибыль по каждой группе предприятий.
Таблица 9.1
Характеристика зависимости прибыли малых предприятий Ростовской обл. от оборачиваемости оборотных средств по состоянию на конец 2000 г.
|
Продолжительность оборота средств, в днях (х) |
Число малых предприятий, ед. |
Средняя прибыль, у.е.(y) |
|
40 - 50 |
6 |
14,57 |
|
51 - 70 |
8 |
12,95 |
|
71 – 101 |
6 |
7,40 |
|
Итого |
20 |
11,77 |
Оборачиваемость в днях – фактор, обозначаемый обычно х, а прибыль – результат – y. Таблица ясно демонстрирует присутствие обратной (отрицательной) связи между признаками.
Говоря об использовании метода группировок для выявления корреляционной зависимости, следует иметь ввиду, что это только прием, при помощи которого можно иллюстрировать наличие или отсутствие связи.
Часто для выявления зависимости между двумя признаками используют
специально построенные корреляционные таблицы:
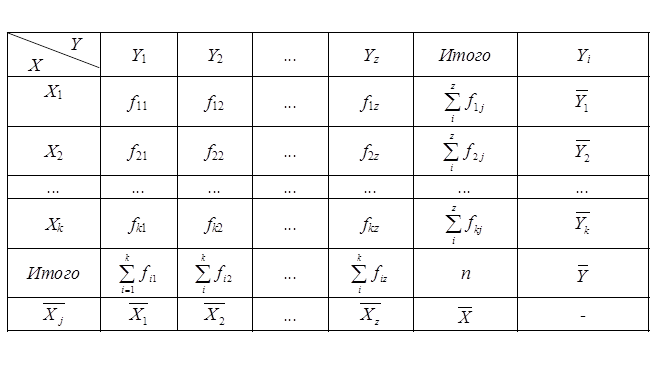
В основу группировки положены два изучаемых во взаимосвязи признака - х и у. Частоты fij показывают количество соответствующих сочетаний х и у. Если fij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания fij допустимо утверждать о связи между x и у. При этом, если fij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.
Графический метод используется для наглядного изображения формы связи между изучаемыми признаками. Для этого в прямоугольных осях координат строят график, по оси ординат которого откладывают индивидуальные значения результативного признака – у, а по оси абсцисс – индивидуальные значения факторного признака – x. Точками показывается сочетание x и у. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи и ее приблизительной форме.
Полученная совокупность точек называется полем корреляции.
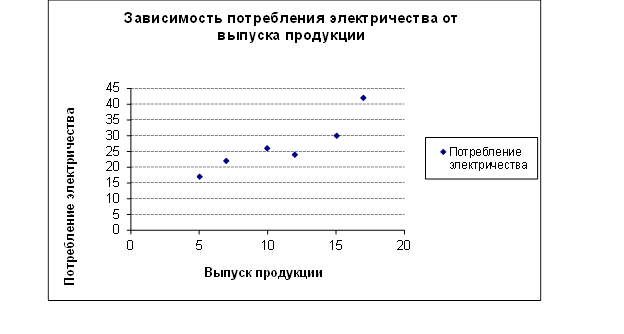
График, построенный по индивидуальным значениям признаков примера, приводимого для параллельного сопоставления рядов, подтверждает то, что связь носит приблизительно линейный характер.
По существу, рассмотренные методы характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов и более глубокого ее изучения и анализа.
| Предыдущая |

