Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.

Предыдущая

Оглавление

Следующая

Глава 9. Статистическое изучение взаимосвязей

9.4. Измерение тесноты связи в случае корреляционной зависимости

Один из простейших показателей тесноты связи разработан австрийским психиатром Г.Фехнером:

,

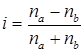где n_a и n_b – соответственно количество совпадений и несовпадений знаков отклонений.

Показатель Фехнера изменяется от –1 до 1, при значении равном 1 он указывает на полную прямую связь, при значении –1 на полную обратную связь, при i=0 связь отсутствует. Промежуточные значения i характеризуют степень близости связи к функциональной. Например, по данным о выпуске продукции (x) на 6 однотипных предприятиях и потреблении на них электроэнергии (у), рассчитаем средние значения для х и у:

;

.

Тогда расчет коэффициента Фехнера для оценки степени зависимости потребления электричества от объема выпуска продукции будет следующим

.

Судя по полученному значению коэффициента, связь можно считать достаточно сильной.

Недостаток показателя Фехнера состоит в том, что разные по абсолютной величине отклонения имеют одинаковый вес. Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции.

Большинство методов измерения тесноты связи заключается в сопоставлении отклонений значений признаков от их средних. Это основано на предположении, что при полной независимости признаков отклонения значений факторного признака от средней  носят случайный характер и должны случайно сочетаться с различными отклонениями . При наличии значительного перевеса совпадений или несовпадений таких отклонений делается предположение о наличии связи между x и y. На этом свойстве основан самый популярный измеритель тесноты связи между признаками – линейный коэффициент корреляции Пирсона (назван по имени английского статистика К.Пирсона, который ввел это коэффициент в научный анализ). Данный коэффициент характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

Что понять смысл (содержание) этого показателя, воспользуемся для расчета данными вышеприведенного примера. Запишем расчеты в виде среднего значения совместных отклонений признаков от их средних значений:

Полученное значение называется коэффициентом ковариации. Это  – мера совместной вариации признаков, т.е. можно сказать, что это мера соответствия вариации результативного признака вариации факторного. Недостатком коэффициента ковариации является то, что он не нормирован. Для преодоления этого недостатка можно полученное выражение разделить на среднее квадратическое отклонение по x и по y  :

.

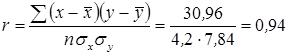Полученное значение есть линейный коэффициент корреляции, показатель интенсивности линейной связи, величина безразмерная, которая изменяется в интервале . Существует эмпирическое правило (шкала Чеддока), согласно которому принято считать, что если r  находится в пределах 0,100 – 0,300, то связь слабая; при  r = 0,300 ¸ 0,500 – умеренная; 0,500 – 0,700 связь заметная; при  r > 0,700 - сильная, или тесная. Когда r = 1 - связь функциональная. Если же r » 0, то это дает основание говорить об отсутствии линейной связи между x и у [4].  

Путем ряда преобразований можно получить следующие аналитические выражения для коэффициента корреляции:

;

.

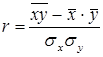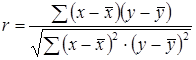Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:

.

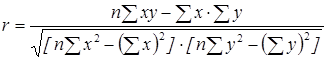Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределения которых близки к нормальному.

Предыдущая

Оглавление

Следующая