Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 9. Статистическое изучение взаимосвязей
9.5. Оценка достоверности коэффициента корреляции
Коэффициент
линейной корреляции, исчисленный по выборочным данным, является случайной
величиной. Полученный из выборки коэффициент корреляции r
является оценкой коэффициента корреляции r в
генеральной совокупности. С уменьшением числа наблюдений надежность
коэффициента корреляции падает. Оценка существенности (значимости)
линейного коэффициента корреляции основана на сопоставлении значения r с его
средней квадратической ошибкой 
:
.
При оценке достоверности коэффициента корреляции обычно рассматриваются следующие ситуации.
1. Если число наблюдений достаточно велико (обычно свыше 50), а значение коэффициента корреляции не превышает 0.9, распределение коэффициента корреляции r можно считать приближенно нормальным со средней квадратической ошибкой:
.
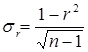При
достаточно большом числе наблюдений r должен превышать свою среднюю
ошибку не менее, чем в три раза: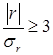 
. Если это неравенство
не выполняется, то существование связи между явлениями нельзя считать
доказанным.
Задавшись
определенной вероятностью, можно построить доверительные границы r: 
.
Так,
например, при вероятности 0,95, для которой t = 1,96,
доверительные границы составят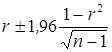 
.
При
вероятности 0,997, для которой коэффициент доверия t = 3, доверительные границы
составят 
.
Поскольку
значение r не может превышать единицу, то в случае, если 
> 1, следует указать только нижний
предел, то есть утверждать, что реальный r не менее,
чем 
.
2. Для малого объема выборки, с распределением r далеким от нормального, применяются другие методы оценки значимости коэффициента корреляции. При небольшом числе наблюдений (n < 30), средняя ошибка линейного коэффициента корреляции находится по формуле:
,
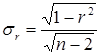а значимость проверяется на основе t критерия Стьюдента. При этом выдвигается гипотеза о равенстве коэффициента корреляции нулю, т.е. об отсутствии связи между x и y в генеральной совокупности. Для этого используется статистика:
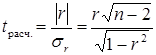
Полученное расчетное значение сопоставляется со значением из таблиц распределения Стьюдента. Если нулевая гипотеза верна, т.е. r=0, то распределение t- критерия подчиняется закону распределения Стьюдента с n-2 степенями свободы и приятым уровнем значимости α (обычно 0,05). Поэтому в каждом конкретном случае по таблице распределения t-критерия Стьюдента находится табличное (критическое) значение t, которое допустимо при справедливости нулевой гипотезы, и с ним сравнивается фактическое (расчетное) значение t. Если tрасч. > tтабл, то нулевая гипотеза отклоняется и линейный коэффициент считается значимым, а связь между x и y – существенной и наоборот.
3. При малом числе наблюдений в выборке и высоком коэффициенте корреляции (распределение r отличается от нормального) для проверки гипотезы о наличии корреляционной связи, а также построения доверительного интервала применяется z-преобразование Фишера.
Для этого рассчитывается величина
.
Распределение
z приближается к нормальному. Вариация z
выражается формулой 
.
Рассчитаем z критерий для рассматриваемого примера, поскольку в этом случае мы имеем небольшое число наблюдений и высокий коэффициент корреляции
.
Чтобы не вычислять значения логарифмов, можно воспользоваться специальными таблицами Z-преобразований [2,4]. Находим, что коэффициенту корреляции 0,94 соответствует Z=1,74.
Находим
Отношение Z к средней квадратической ошибке равно 3. Таким образом, мы можем полагать действительное наличие связи между величиной выпуска продукции и расходом электроэнергии для всей совокупности предприятий.
| Предыдущая |