Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 9. Статистическое изучение взаимосвязей
9.7. Парная линейная регрессия
Для характеристики влияния изменений х на вариацию у служат методы регрессионного анализа. Регрессия – это линия, показывающая вид зависимости средней результативного признака от факторного. Термин, введенный английским статистиком Гальтоном при изучении наследственности. Уравнение регрессии является аналитическим уравнением, с помощью которого выражается связь между признаками. В случае парной линейной зависимости строится регрессионная модель
![]() ,
,
где n - число наблюдений; а0, а1 - неизвестные параметры уравнения;
ei - ошибка случайной переменной Y.
Уравнение регрессии записывается как:
Yiтеор=a0 +a1Xi,
где Yiтеор - рассчитанное выравненное значение результативного признака после подстановки в уравнение X.
Параметры а0 и а1 оцениваются с помощью процедур, наибольшее распространение из которых получил метод наименьших квадратов. Линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной. Значит, наилучшие оценки a0 и а1, получают, когда
![]()
т.е. сумма квадратов отклонений эмпирических значений зависимой переменной от вычисленных по уравнению регрессии должна быть минимальной. Сумма квадратов отклонений является функцией параметров а0 и а1. Ее минимизация осуществляется решением системы уравнений
![]() ;
;
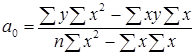 ;
; 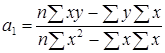 .
.
Можно воспользоваться и другими формулами, вытекающими из метода наименьших квадратов, например:
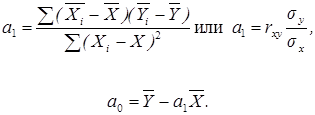
Аппарат линейной регрессии достаточно хорошо разработан и, как правило, имеется в наборе стандартных программ оценки взаимосвязи для ЭВМ. Важен смысл параметров: а1 – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение X на Y. Он показывает, на сколько единиц в среднем изменится Y при изменении X на одну единицу. Если а, больше 0. то наблюдается положительная связь. Если а имеет отрицательное значение, то увеличение X на единицу влечет за собой уменьшение Y в среднем на а1. Параметр а1 обладает размерностью отношения Y к X.
Параметр a0 – это постоянная величина в уравнении регрессии. На наш взгляд, экономического смысла он не имеет, но в ряде случаев его интерпретируют как начальное значение Y.
Значение функции Yтеор = a0 + а1X называется расчетным значением и на графике образует теоретическую линию регрессии. Смысл теоретической регрессии в том, что это оценка среднего значения переменной Y для заданного значения X.
Например, рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда Y от стажа работы X по представленным данным о бригаде из десяти рабочих, занятых производством электротехнических изделий. Для расчета коэффициентов уравнения регрессии воспользуемся расчетной таблицей:
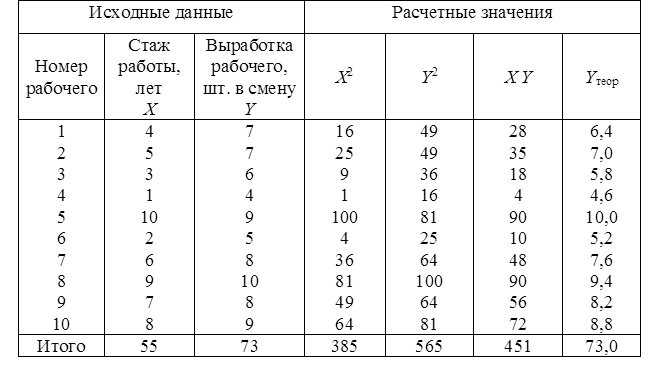
Расчетные значения подставим в формулу и получим параметры для данного уравнения регрессии:
![]() ;
;
![]() .
.
Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера имеет вид: Yтеор= 4 + 0.6X.
Это уравнение характеризует зависимость среднего уровня выработки рабочим бригады от стажа работы.
Парная корреляция или парная регрессия могут рассматриваться как частный случай отражения связи некоторой зависимой переменной, с одной стороны, и одной из множества независимых переменных – с другой. Когда же требуется охарактеризовать связь всего указанного множества независимых переменных с результативным признаком, говорят о множественной корреляции или множественной регрессии.
Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя (важным условием является отсутствие между факторами функциональной связи).
Для оценки взаимосвязи между признаком Y и несколькими факторными признаками Xi используется коэффициент множественной корреляции (совокупный коэффициент корреляции, коэффициент детерминации). Для случая двух факторных признаков x1 и x2 он имеет вид:
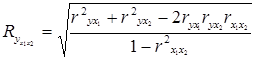 ,
,
где r – парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется от 0 до 1 и численно не может быть меньше, чем любой из образующих его парных коэффициентов. Приближение R к единице свидетельствует о сильной зависимости между признаками.
При небольшом числе наблюдений величина коэффициента множественной корреляции, как правило, завышается. Чтобы оценить общую вариацию результативного признака в зависимости от факторных признаков, величина коэффициента множественной корреляции корректируется на основании следующего выражения:
![]() ,
,
где ![]() -
скорректированное значение; n – число наблюдений;
-
скорректированное значение; n – число наблюдений;
k – число факторных признаков.
Корректировку можно не производить, если ![]()
Среднеквадратическая ошибка коэффициента множественной корреляции:
![]() ,
,
если ![]() > 3, то с
вероятностью близкой к 0,99 можно считать R значимым.
> 3, то с
вероятностью близкой к 0,99 можно считать R значимым.
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками при фиксированном значении всех остальных.
Для случая двух факторных признаков x1 и x2 они имеют вид:
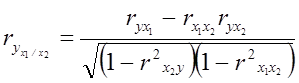 ;
;
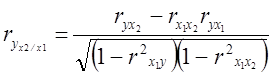 .
.
В первом случае исключено влияние факторного признака x2, а во втором x1. Значения парного и частного коэффициентов корреляции отличаются друг от друга, так как парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный учитывает наличие и влияние других факторов.
Проверка значимости и расчет доверительных интервалов для частных коэффициентов корреляции аналогичны, как и для парных коэффициентов корреляции, с тем лишь отличием, что число степеней свободы n определяется так: n = n - k, где k – порядок коэффициента частной корреляции.
| Предыдущая |

