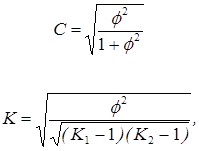Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 9. Статистическое изучение взаимосвязей
9.6. Непараметрические методы оценки связи
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.
Между тем в статистической практике изучения общественных явлений приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.
Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемых таблиц взаимной сопряженности.
Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.

Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т. д.
Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т. д.
Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):
где f2 - показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
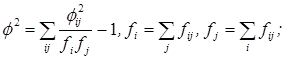
К1 и К2 - число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.
Измерение связи между альтернативными признаками, т.е. признаками, принимающими только два возможных значения (дихотомические). Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводятся значения признаков.
|
A |
B |
|
C |
D |
Например, требуется измерить связь между прививками от гриппа и пониженной заболеваемостью от гриппа в группе случайно выбранных студентов.
|
Заболели |
Не заболели |
Итого |
|
Привитые |
30 |
20 |
50 |
|
Не привитые |
15 |
5 |
20 |
|
Итого |
45 |
25 |
70 |
Существует ли связь между заболеваемостью и прививками? Для измерения тесноты взаимосвязи признаков производится расчет коэффициента контингенции по формуле:
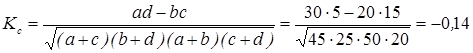 .
.
Коэффициент контингенции принимает значения в интервале от –1 до 1, а интерпретация аналогична коэффициенту корреляции. Судя по значению коэффициента связь между заболеваемостью и прививками слабая отрицательная.
Другой метод измерения связи основан на расчете коэффициента ассоциации:
![]() .
.
Минус перед коэффициентом говорит об обратном направлении связи, т.е. чем больше прививок, тем меньше заболеваний. Коэффициент контингенции всегда бывает меньше коэффициента ассоциации и дает более корректную оценку тесноты связи.
Например, в результате обследования работников предприятия получены следующие данные (чел.):
|
Образование |
Удовлетворены работой |
Не удовлетворены работой |
Итого |
|
Высшее и среднее |
300 |
50 |
350 |
|
Незаконченное среднее |
200 |
250 |
450 |
|
Итого |
500 |
300 |
800 |
Требуется оценить тесноту взаимосвязи между уровнем образования и удовлетворенностью своей работой с помощью коэффициентов контингенции и ассоциации.
Коэффициент ассоциации:
![]() .
.
Коэффициент контингенции:
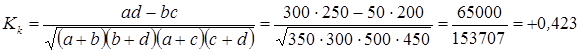 .
.
Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т. д.
При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
Если n вариантов ряда расположены в соответствии с возрастанием или убыванием признака x, то говорят, что объекты ранжированы по этому признаку. Ранг xi указывает место, которое занимает i-е значение признака среди других n значений признака x (i=1,2,..n).
Например, при исследовании рынка мы можем задать вопрос с целью выяснения предпочтений потребителей при выборе товара (при покупке акций, мороженного, пива и т.п.), таким образом, чтобы они распределили товар в порядке возрастания (или убывания) своих потребительских предпочтений. Если мы имеем два набора ранжированных данных, то можно попытаться установить степень линейной зависимости между ними. Предположим мы имеем 5 продуктов, которые ранжированы по порядку предпочтений от 1 до 5 в соответствии с двумя характеристиками А и В.
|
Характеристики для ранжирования |
Продукты |
||||
|
Z |
V |
W |
X |
Y |
|
|
A |
4 |
2 |
5 |
1 |
3 |
|
B |
5 |
1 |
3 |
2 |
4 |
Использование для определения интенсивности связи между признаками коэффициента Пирсона будет не верным, так как он применяется для признаков, измеряемых на количественных шкалах. Например, при измерении взаимосвязи между ростом и весом, мы измеряет рост в см. а вес в кг., при этом можно точно определить на шкале измерений разницу в значении этих признаков для любого человека.
Для определения наличия взаимосвязи между ранговыми оценками используется коэффициент ранговой корреляции Спирмена. Его расчет основан на различиях между рангами. Обозначим D = ранг A – ранг B.
Коэффициент
Спирмена равен: 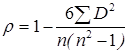 ,
,
где n – число пар ранжированных наблюдений.
В нашем примере мы имеем пять пар рангов, следовательно, n = 5. Cумма D2 равна: (2-1)2 + (5-3)2 + (1-2)2 + (3-4)2 + (4-5)2=1+4+1+1+1=8
Коэффициент Спирмена равен:
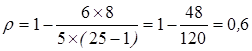 .
.
Значит мы нашли умеренно сильную линейную связь. Коэффициент Спирмена изменяется в интервале от –1 до 1 и интерпретируется так же как и коэффициент Пирсона. Разница лишь в том. что он вычисляется для ранжированных данных.
Значимость
коэффициента Спирмена проверяется на основе t критерия
Стьюдента по формуле: 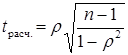 .
.
Значение коэффициента считается существенным, если tрасч. > tкрит. (a; k = n-2).
Коэффициент корреляции рангов может быть рассчитан и по формуле, предложенной английским статистиком М.Кендаллом:
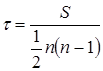 ,
,
где S- фактическая сумма рангов; ![]() -
максимальная сумма рангов.
-
максимальная сумма рангов.
Этот коэффициент изменяется в интервале от –1 до 1 и
интерпретируется также как и коэффициент Пирсона, но он дает более строгую
оценку связи, чем коэффициент Спирмена ![]() . Это
соотношение выполняется при большом числе наблюдений,
. Это
соотношение выполняется при большом числе наблюдений, ![]() ,
и слабых либо умеренно тесных связях.
,
и слабых либо умеренно тесных связях.
Рассмотрим порядок расчета коэффициента Кендалла на
предыдущем примере. Для расчета τ все единицы ранжируются по признаку
А; по ряду признака В подсчитывается для каждого ранга число последующих
рангов, превышающих данный (их сумму обозначим Р), и число последующих
рангов ниже данного (их сумму обозначим Q).
Тогда S = P – Q. Можно показать, что ![]() , так
что τ может быть представлен как:
, так
что τ может быть представлен как:
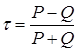 .
.
|
Характеристики для ранжирования |
Продукты |
||||
|
Z |
V |
W |
X |
Y |
|
|
A |
4 |
2 |
5 |
1 |
3 |
|
B |
5 |
1 |
3 |
2 |
4 |
Преобразуем ряд
|
Характеристики для ранжирования |
Продукты |
||||
|
Z |
V |
W |
X |
Y |
|
|
A |
5 |
1 |
2 |
3 |
4 |
|
B |
3 |
2 |
1 |
4 |
5 |
S= (3-1)+(3-0)+(1-1)+(0-1)=4; 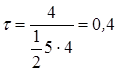 .
.
Действительно, если полученное значение τ умножить на 1,5, то получим 0,6 – значение коэффициента Спирмена.
Существенность коэффицента корреляции рангов Кенделла проверяется по формуле:
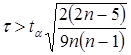 ,
,
где tα- коэффициент, определяемый по таблице нормального распределения для выбранного уровня значимости α при больших n.
| Предыдущая |