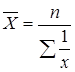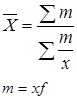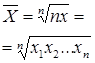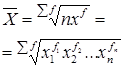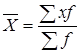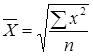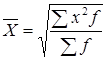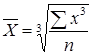Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.

Предыдущая

Оглавление

Следующая

Глава 5. Средние величины

5.2. Виды средних и способы их вычисления

Рассмотрим теперь виды средних величин, особенности их исчисления и области применения. Средние величины делятся на два больших класса: степенные средние, структурные средние.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

В качестве структурных средних рассматриваются мода и медиана.

Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.

Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:

,

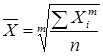где X_i – варианта (значение) осредняемого признака;

m – показатель степени средней; n – число вариант.

Взвешенная средняя считается по сгруппированным данным и имеет общий вид

,

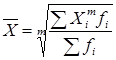где X_i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

m – показатель степени средней;

f_i – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:

средняя гармоническая, если m = -1;

средняя геометрическая, если m® 0;

средняя арифметическая, если m = 1;

средняя квадратическая, если m = 2;

средняя кубическая, если m = 3.

Формулы степенных средних приведены в табл. 5.1.

Таблица 5.1

Виды степенных средних

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средняя арифметическая и средняя гармоническая взвешенные. Выбор вида степенной средней определяется экономическим содержанием задачи и наличием данных.

Рассмотрим, известные вам, среднюю арифметическую простую и взвешенную. Приведем в качестве примера расчет среднего возраста студентов в группе из 10 человек:

Средний возраст рассчитаем по формуле простой средней:

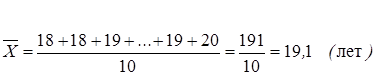
Сгруппируем исходные данные. Получим следующий ряд распределения:

В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте Х лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:

Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую чаще всего применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е.  m = X·f).

Например, есть данные о реализации продукта одного вида на трех рынках города:

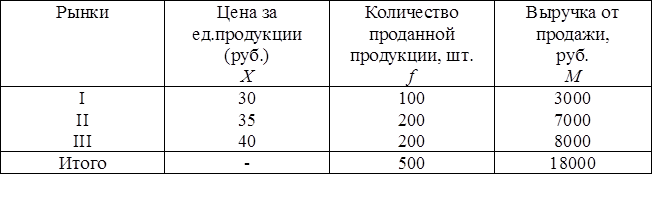
Требуется рассчитать среднюю цену, по которой продавался товар.

При расчете средней цены на один и тот же товар, который продается в трех разных торговых точках, необходимо выручку от реализации продукции поделить на количество реализованной продукции.

Предположим, мы располагаем только данными о ценах на трех рынках и о количестве товара, проданного на каждом их них. При этом цены на отдельных рынках выступают в качестве вариантов, а количество проданного товара – в качестве весов. Тогда средняя цена определится по средней арифметической взвешенной, то есть

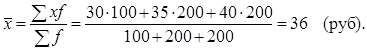
Теперь предположим, что количество проданного товара неизвестно, а известны лишь цены и выручка от продажи. В этом случае логические рассуждения остаются теми же, но расчет следует записать в форме средней гармонической взвешенной.

Чтобы исчислить среднюю, обозначим x·f=М, откуда f=М/x. Преобразуем формулу средней арифметической так, чтобы по имеющимся данным x и М можно было исчислить среднюю.

В формулу средней арифметической взвешенной вместо x·f подставим М, вместо f – отношение М/x и получим формулу средней гармонической взвешенной:

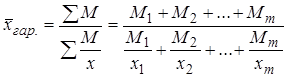
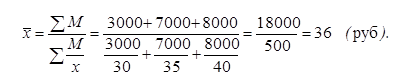
Результат, как и следовало ожидать, получился тот же.

Рассмотрим еще один пример расчета средней гармонической взвешенной. Допустим, в результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было 3942 кг., что составляет 70,4% общего веса муки этой партии. Во второй партии муки высшего сорта было 6520 кг., что составляет 78,6% общего веса муки этой партии. Необходимо определить процент муки высшего сорта в среднем по первой и второй партиям вместе.

Средний процент муки высшего сорта по двум партиям определяем по формуле средней гармонической взвешенной:

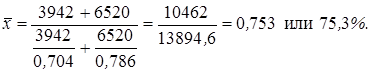
В том случае, если объемы явлений, т.е. произведения, по каждому признаку равны, применяется средняя гармоническая простая. К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.

         Например, две автомашины прошли один и тот же путь: одна со скоростью 60 км/час, а вторая – 80 км/час. Тогда средняя скорость составит:

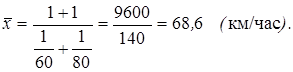
Таким образом:

,

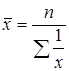где  - сумма обратных значений вариант;         n – число вариант.

Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии.

Предположим, произведены инвестиции, приносящие ежегодный доход, процент которого от года к году различается. Например, в течение 5 лет % дохода за первый год есть i₁ , за второй год - i₂, за третий год -i₃, за четвертый год – i₄ , за пятый год – i₅  Доход на инвестиции начисляется один раз в год. После каждого года сумма, равная процентному приросту, добавляется к сумме счета.

Необходимо вычислить средний уровень дохода за пять лет.

Можно сложить i₁, i₂, i₃, i₄, i₅ и разделить на 5. Полученная величина будет арифметической средней уровня дохода за 5 лет.

Однако, заметим следующее. Если первоначальная сумма инвестиций - Р, то после первого года она возрастает и становится P(1+i₁). В конце второго года эта сумма составит P^.(1+i₁)(1+i₂) и так далее. По истечении пяти лет сумма составит F=P^.(1+i₁)(1+i₂)(1+i₃)(1+i₄)(1+i₅). Если мы хотим определить средний процент дохода i, который даст нам сумму дохода F по истечении пяти лет при прибавлении ежегодного накопленного прироста к сумме вклада, то рассчитаем коэффициент, который находится из следующего уравнения:

(i+1)⁵ = (1+i₁)^.(1+i₂)^.(1+i₃)^.(1+i₄)^.(1+i₅).

Решение этого уравнения находится по формуле:

,

где (i+1) - геометрическая средняя из (1+i₁), (1+i₂), (1+i₃), (1+i₄), (1+i₅).

Предположим, что n = 2 года, i₁ = 0,10 и i₂  = 0,05.

Геометрическая средняя от  (1+i₁) и (1+i₂) есть:

Эта средняя дает рост по вкладу за два года – 0,0747 или 7,47%. Если бы мы рассчитывали среднюю арифметическую, то получили бы

x = (0,10 + 0,05) / 2 = 0,075,

что несколько отличается от геометрической средней. Разница в данном примере невелика, но расчет по формуле средней геометрической более верен.

Важно знать не только формальные методы исчисления средних величин, но и правила корректного выбора средней. Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым^[2]. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины.

---

Предыдущая

Оглавление

Следующая