Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 6. Показатели вариации (рассеяния)
6.3. Показатели относительного рассеяния
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеяния в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеяния осуществляют как отношение абсолютного показателя вариации признака к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
.
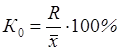2. Относительное линейное отклонение характеризует долю усредненного значения признака абсолютных отклонений от средней величины:
.
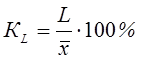3. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин:
.
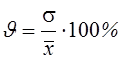Предположим, что стандартное отклонение в выборке валютных счетов в банке «А» и банке «В» равно $20. Данные по банку «А» содержат информацию о счетах, сумма которых находится в пределах $60. В банке «В» данные содержат информацию относительно счетов, сумма которых достигает $1 миллион и больше. В первом случае стандартное отклонение в 20 единиц очень велико относительно сумм счетов. Для суммы порядка $1 миллиона – что значит вариация плюс-минус $20 относительно среднего? Конечно, такая вариация будет «каплей в море». Сравнивая эти два случая, можно сказать, что такая абсолютная мера рассеяния как стандартное отклонение не передает существенной информации при сравнении вариационных рядов. Коэффициент вариации создан специально как относительная мера вариации.
Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя. В статистике совокупности, имеющие коэффициент вариации больше 30-35 %, принято считать неоднородными.
Однако
у такого способа оценки вариации есть и существенный недостаток. Например,
исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением s = 10 лет,
«состарилась» еще на 15 лет. Теперь 
= 30 лет, а среднеквадратическое
отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15 × 100 = 66,7%), со временем оказывается, таким
образом, вполне однородной (10/30 × 100 = 33,3 %).
Рассмотрим пример расчета средней дневной заработной платы для работников предприятия и показателей вариации рабочих по зарплате.
|
Заработная плата, руб. |
Число рабочих, F |
x |
x∙f |
|
|
|
|
|
До 180 |
5 |
170 |
850 |
73 |
365 |
5329 |
26645 |
|
180-200 |
10 |
190 |
1900 |
53 |
530 |
2809 |
28090 |
|
200-220 |
15 |
210 |
3150 |
33 |
495 |
1089 |
16335 |
|
220-240 |
20 |
230 |
4600 |
13 |
260 |
169 |
3380 |
|
240-260 |
25 |
250 |
6250 |
7 |
175 |
49 |
1225 |
|
260-280 |
20 |
220 |
5400 |
27 |
540 |
729 |
14580 |
|
280-300 |
20 |
290 |
5800 |
47 |
940 |
2209 |
44180 |
|
ИТОГО: |
115 |
|
27950 |
|
3305 |
|
134435 |
Средняя
дневная заработная плата: 
= 27950/115=243 руб.
Среднее
линейное отклонение: 
Следовательно, средняя заработная плата за смену колеблется в пределах от 214,3 до 271,7 руб (`Х=243±28,7).
Дисперсия:
Средний квадрат отклонений заработной платы от ее средней величины составляет 1169 руб. Среднее квадратическое отклонение:
Средняя дневная заработная плата рабочих колеблется в пределах от 208,8 до 277,2 руб (`Х=243±34,2 руб.).
Коэффициент вариации:
V = (34,2/243)× 100=14,1%.
Величина коэффициента вариации небольшая, следовательно, разброс значений заработной платы около ее средней невелик, таким образом, можно сделать вывод, что совокупность однородна по составу, а средняя вполне представительна.
| Предыдущая |