Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 6. Показатели вариации (рассеяния)
6.4. Меры вариации для сгруппированных данных. Правило сложения дисперсий
Вариация признаков, как правило, обусловлена влиянием различных факторов. Если совокупность разбить на группы по факторному признаку, то это окажет определенное влияние на значение вариации признака в группах. Выявить долю вариации, определяемую теми или иными факторами, можно, разделив всю совокупность на группы по фактору, влияние которого исследуется. Чаще всего для этих целей используются показатели вариации для сгруппированных данных. В этом случае выделяют три вида дисперсий: общую дисперсию; внутригрупповую дисперсию, межгрупповую дисперсию.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов. Внутригрупповая дисперсия измеряет вариацию признака внутри группы, а межгрупповая дисперсия измеряет вариацию групповых средних относительно общей средней.
Существует закон, связывающий три вида дисперсии:
Общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:
,
где внутригрупповая дисперсия, которая рассчитывается по формуле:
,
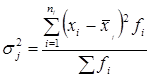– групповая
средняя, 
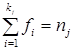– объем j-й группы.
Суммирование и в числителе, и в знаменателе осуществляется только по тем значениям признака, которые попали в j группу.
Средняя из внутригрупповых дисперсий:
,
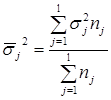nj – число значений признака в группе j, сумма nj равна n - общему числу значений признаков ряда, l – число групп.
,
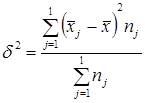где 
- общая средняя
вариационного ряда, 
- число значений признаков в
группе j. Она
измеряет вариацию, обусловленную признаком, положенным в основу группировки.
Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, формируется из дисперсии, возникающей за счет фактора группировки и дисперсии, возникающей под воздействием всех прочих факторов.
С помощью закона сложения дисперсий можно оценить удельный вес факторов, лежащих в основе группировки, во всей совокупности факторов, воздействующих на результативный признак. Для этого применяется коэффициент детерминации, который рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака:
.
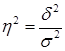Корень квадратный из коэффициента детерминации называют эмпирическим корреляционным отношением:
.
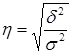Эмпирическое корреляционное отношение показывает какую часть общей колеблемости результативного признака определяет изучаемый фактор, т.е. характеризует влияние группировочного признака на результативный признак. Этот показатель принимает значения в интервале [0,1]. Если связь отсутствует, то h = 0. В этом случае дисперсия групповых средних равна нулю (d2 = 0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то h = 1. В этом случае дисперсия групповых средних равна общей дисперсии (d2 = s2), т.е. не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака, а влияние прочих факторных признаков равно нулю. Промежуточные значения h оцениваются по степени их близости к предельным.
Допустим, большая торговая компания заказала опрос с целью выяснения влияния фактора повышения квалификации на результаты работы агентов по продажам. Опрос 8 торговых агентов дал следующие результаты:
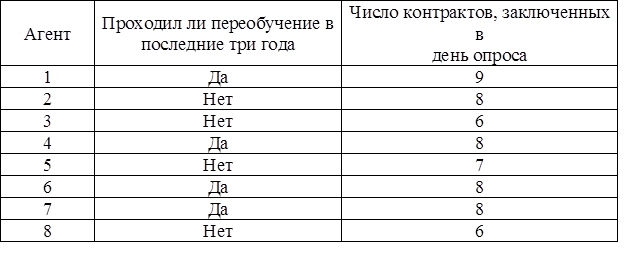
Среднее число контрактов, заключенных агентами:
.
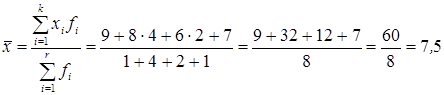В данном примере переподготовка рассматривается как факторный признак, а число заключаемых контрактов – как результативный.
Сгруппируем эти данные по признаку переобучения и рассчитаем средние по каждой группе.
|
Группы агентов |
Число агентов |
Число контрактов |
Групповая средняя |
|
Прошли переобучение |
4 |
9, 8, 8, 8 |
8,25 |
|
Не прошли переобучение |
4 |
8, 6, 7, 6 |
6,75 |
,
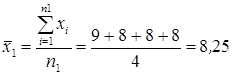где n1 – число признаков в первой группе.
Или по формуле для взвешенных вариант
,
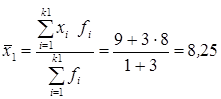где fi – частоты ряда.
,
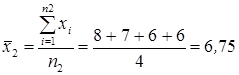где n2 – число признаков во второй группе.
Рассчитаем дисперсию в каждой группе.
Дисперсия числа заключенных контрактов у агентов, прошедших переобучение:
|
Число контрактов Х |
Частота f |
|
|
|
|
9 8 |
1 3 |
0,75 - 0,25 |
0,5625 0,0625 |
0,5625 0,1875 |
|
Итого |
4 |
- |
- |
0,7500 |
.
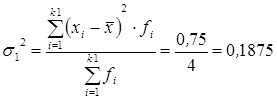Дисперсия числа заключенных контрактов у агентов, не прошедших переобучение:
|
Число контрактов Х |
Частота f |
|
|
|
|
8 7 6 |
1 1 2 |
1,25 0,25 - 0,75 |
1,5625 0,0625 0,5625 |
1,5625 0,0625 1,1250 |
|
Итого |
4 |
- |
- |
2,7500 |
.
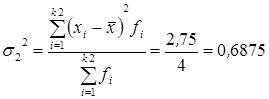Рассчитаем среднюю из внутригрупповых дисперсий:
.
Этот показатель характеризует влияние на результативный признак всех прочих факторных признаков за исключением признака, положенного в основу группировки.
Очевидно, что различие в числе заключенных контрактов в двух группах вызвано тем, что брокеры первой группы прошли переобучение, а брокеры второй группы не прошли. Найдем дисперсию между группами (межгрупповую дисперсию). Согласно формуле :
.
Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки.
Общая
дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий: 
=0.
Проверим верность правила сложения дисперсий. Рассчитаем общую дисперсию числа заключенных контрактов
|
Число контрактов Х |
Частота F |
|
|
|
|
9 8 7 6 |
1 4 1 2 |
1,5 0,5 -0,5 -1,5 |
2,25 0,25 0,25 2,25 |
2,25 1,00 0,25 4,50 |
|
Итого |
8 |
- |
- |
8,00 |
s2 = 8/8 = 1,00
В самом деле, 1,00 = 0,5625 + 0,4375.
По данным примера эмпирическое корреляционное отношение равно:
.
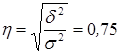Следовательно, фактор, положенный в основу группировки, существенно влияет на число заключаемых агентами контрактов, но существуют и другие факторы, влияние которых тоже заметно.
| Предыдущая |