Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 6. Показатели вариации (рассеяния)
6.5. Вариация альтернативного признака
Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Напомним, что альтернативный признак – это признак, который может принимать только два возможных значения: 1 или 0.
Внутригрупповая дисперсия доли определяется по формуле
![]() .
.
Средняя из внутригрупповых дисперсий рассчитывается так:
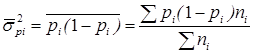 .
.
Формула межгрупповой дисперсии имеет следующий вид:
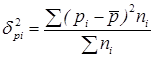 ,
,
где ni – численность единиц в отдельных группах;
р – доля изучаемого признака во всей совокупности, которая определяется по формуле:
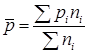 .
.
Общая дисперсия определяется по формуле:
![]()
Три вида дисперсий объединены между собой следующим образом:
![]() .
.
Это – правило сложения дисперсии доли признака.
Допустим, имеются следующие данные об удельном весе основных рабочих в трех цехах фирмы:
|
Цех |
Удельный вес основных рабочих в % (pi) |
Численность всех рабочих, чел. |
|
1 2 3 |
80 75 90 |
100 200 150 |
|
Итого |
- |
450 |
Определим долю рабочих в целом по фирме (4):
![]() .
.
Общая дисперсия доли основных рабочих по всей фирме в целом будет равна (5):
![]() .
.
Внутрицеховые дисперсии рассчитаем, применив формулу 1:
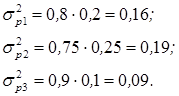
Средняя из внутригрупповых дисперсий будет равна (2):
![]() .
.
Межгрупповую дисперсию определим по формуле 3:
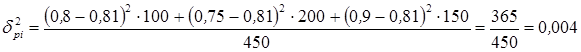 .
.
Проверка вычислений показывает: 0,154 = 0,15 + 0,004.
| Предыдущая |

