Д.В. Арутюнова
Инновационный менеджмент
Учебное пособие. – Ростов-на-Дону: Изд-во ЮФУ, 2014. – 152 с.
| Предыдущая |
Тема 7. Планирование и управление программами НИОКР
7.4. Оценка и планирование портфеля проектов
Изложенное выше касалось оценки отдельных проектов НИОКР. Практически вопрос обычно стоит значительно шире: надо выбрать оптимальный в некотором смысле набор НИОКР.
Портфель НИОКР может состоять из разнообразных проектов крупные и мелкие; близкие к завершению и начинающиеся. Однако, каждый требует выделения дефицитных ресурсов в зависимости от особенностей проекта (сложности, трудоемкости и т. п.).
Портфель должен иметь определенные контуры, быть стабильным, чтобы рабочая программа могла осуществляться равномерно.
Количество проектов, находящихся в портфеле в конкретный период времени, зависит от размеров проектов, которые измеряются через общий объем ресурсов, необходимых для разработки и затрат на реализацию одного проекта. Часть проектов будет прекращена в процессе выполнения, их составные части будут меняться по числу и потребности в ресурсах и т.д.
Ни одна из инвестиционных возможностей не должна рассматриваться изолированно от всего портфеля инвестиций (на диверсификацию компании, расширение и модернизацию производства, НИОКР). Портфель НИОКР постоянно меняется. Его содержание всегда зависит от прошлых решений, однако балансировка требует появления новых проектов. Таким образом, процесс планирования и корректировки планов НИОКР непрерывен.
По мнению специалистов, только 10% всех проектов являются полностью успешными. Это означает, что существует только 10% вероятность эффективного завершения каждого проекта из портфеля. Вместе с тем необходимо учитывать риск, связанный с проектами НИОКР, так проекты могут быть неуспешными в зависимости от отрасли либо по техническим, либо по коммерческим причинам.
Оптимизация портфеля НИОКР фирмы в стратегическом смысле начинается с решения коренной задачи: каким должен быть оптимальный баланс между исследованиями (НИР) и разработками (ОКР). Столь же важно и решение вопроса оптимального размещения капиталовложений в НИОКР и на приобретение готовой продукции. Если фундаментальные знания, полученные от научных исследований, и новые технологии в результате инвестиций в разработки дают нам больше шансов в неопределенном будущем, то приобретение готовой техники дает определенную выгоду уже сегодня. Естественно, что эти обстоятельства следует учитывать при принятии решений о финансировании НИОКР и стратегии закупок.
Преимущество небольших проектов в том, что они легче адаптируются друг к другу в отношении соответствия наличным ресурсам. Крупный проект требует большого объема ресурсов.
Однако небольшие проекты (требующие относительно небольших затрат на НИОКР) обычно реализуются в новых продуктах, имеющих скромный потенциал по объему продаж (и потенциал прибыли). Портфель небольших проектов может привести к равномерному потоку нововведений, большая часть из которых обладает ограниченным рыночным потенциалом, что нежелательно с позиций номенклатуры продукции, формируемой отделами маркетинга.
Проекты разбиты на этапы, и искусство управления состоит в распределении их запуска во времени с целью обеспечения эффективности всего портфеля. В табл. 1 приведено сравнение денежных потоков двух вариантов запуска проектов: параллельного и последовательного. В этом случае последовательная реализация обеспечивает такие преимущества:
- управленческие усилия в каждый момент времени затрачиваются на один проект;
- любая задержка по проекту А не требует перераспределения ресурсов внутри портфеля;
- новый продукт А начинается производством на два года раньше, увеличивается его жизненный цикл, коммерческие и финансовые эффекты, связанные с более ранним выходом на рынок;
- проект Б может начаться на более совершенной научно-технической базе с использованием уточненной рыночной информации;
- выравнивается сальдо денежных потоков в 3-й и 4-й годы.
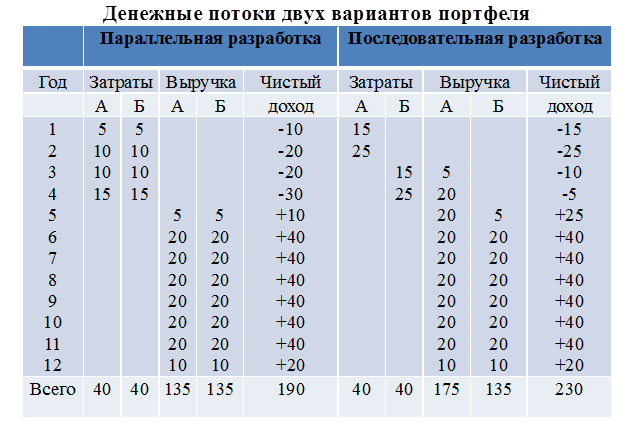
При всей своей искусственности пример показывает целесообразность концентрации усилий в НИОКР. Очередность выполнения проектов необязательно связана с их экономической значимостью. Например, возможна такая ситуация, что следует запустить в первую очередь менее значимый проект с более коротким временем жизненного цикла товара, иначе экономическая выгода от его реализации резко сократится.
При планировании конкретных проектов используются ленточные и сетевые графики. Следует обратить внимание на следующие важные положения планирования:
- распределение ресурсов в увязке со всем портфелем;
- определение программы работ, ресурсов, времени;
- выявление решающих "критических точек";
- выделение главнейших задач;
- увязка графика работ с "критическими точками";
- интеграция всех видов деятельности в рамках общего плана.
Задачу формирования «портфеля» проектов удобно представить в виде распределительной задачи, которая связана с распределением ресурсов по проектам, которые необходимо выполнить в рамках портфеля. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждого проекта наиболее эффективным образом. Поэтому целью решения задачи этого типа является отыскание такого распределения ресурсов по проектам, при котором либо минимизируются общие затраты, связанные с выполнением проектов, либо максимизируется получаемый в результате общий доход.
Большинство распределительных задач можно представить в виде матриц, приведенных в таблице.
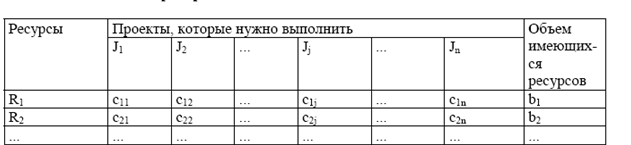

Особенности управлении я портфелем проектов:
1. Величины cij могут быть независимыми или зависимыми.
2. Распределение ресурсов для одного периода времени может влиять на распределения ресурсов для последующих периодов, а может не оказывать на них никакого влияния.
Если каждое из последовательности распределений не зависит от всех остальных, то такая задача называется статической, в противном случае имеем динамическую распределительную задачу. Статические задачи исследованы в большей степени, чем динамические, но для решения некоторых типов динамических задач успешно применяются методы линейного программирования. Для решения некоторых динамических задач применяются методы стохастического программирования. В таких задачах решение основано на вероятностных оценках будущих значений параметров (например, удельных затрат, продажной цены, спроса и т.д.), имеющих фиксированное распределение вероятностей.
1. Основные методы решения распределительных задач, в частности ЛП, построены на допущении, что объемы имеющихся в наличии ресурсов (bi), требуемые объемы (aj) и затраты (cij) точно известны. Однако на самом деле в оценках этих величин возможны ошибки. Поэтому иногда требуется выяснить, насколько чувствительно решение распределительной задачи к возможным ошибкам указанных величин, выступающих в качестве коэффициентов.
2. Если общий объем наличных ресурсов равен общей потребности в них, то имеет место сбалансированная (закрытая) распределительная задача:
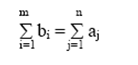
Если 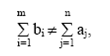 , то задача
называется несбалансированной (открытой) и требуется не только распределить
ресурсы по проектам, но решить также какие проекты не будут реализованы, либо
какие ресурсы не использовать в процессе реализации портфеля.
, то задача
называется несбалансированной (открытой) и требуется не только распределить
ресурсы по проектам, но решить также какие проекты не будут реализованы, либо
какие ресурсы не использовать в процессе реализации портфеля.
При недостатке ресурсов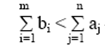 ,
,
При избытке ресурсов 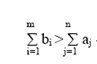 .
.
Рассматривая тот или иной проект на предмет включения в портфель, необходимо учитывать возможное качество управления и последствия перераспределения затрат на проекты.
Для примера оценим два портфеля, состоящие из двух проектов (табл.2.). Оба портфеля небольшие.
Таблица 2
Оценка эффективности портфелей
|
Проект |
Портфель А |
||
|
1 |
2 |
3 |
|
|
Затраты ден.ед. |
Прибыль ден.ед |
Рентабельность |
|
|
1 |
22000 |
41800 |
1,9 |
|
2 |
18000 |
32600 |
1,8 |
|
Общая оценка портфеля |
40000 |
74400 |
1,86 |
|
Проект |
Портфель Б |
||
|
3 |
4 |
5 |
|
|
Затраты ден.ед. |
Прибыль ден.ед |
Рентабельность |
|
|
1 |
34000 |
59500 |
1,75 |
|
2 |
30000 |
57000 |
1,9 |
|
Общая оценка портфеля |
64000 |
116500 |
1,82 |
Рентабельность портфеля (прибыльность) определяется как отношение прибыли к затратам.
Первый проект, входящий в портфель А, рентабельнее проекта, входящего в портфель Б, на 8,6% (1,9 / 1,75 = 1,086), но второй проект более рентабелен в портфеле Б (1,8 / 1,9 = 0,947), т. е. рентабельность второго проекта в портфеле А ниже на 9,5%.
Общая оценка портфелей дается по показателям средней
рентабельности. Обозначим рентабельность портфелей А Б соответственно ![]() и
и ![]() .
.
Рентабельность отдельных проектов, как видно из табл.3.1,
определяется так:![]()
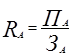 ,
,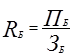 .
(3.1)
.
(3.1)
Средняя рентабельность портфелей
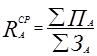 ,
, 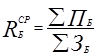 .
(3.2)
.
(3.2)
На основе показателей рентабельности может быть рассчитан
коэффициент предпочтения ![]() :
:
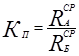 (3.3)
(3.3)
В нашем примере коэффициент предпочтения
![]()
или 2,2%.
| Предыдущая |

