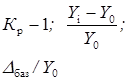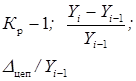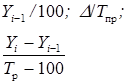Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 7. Статистическое изучение динамики общественных явлений
7.3. Показатели анализа рядов динамики
При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Большинство статистических характеристик ряда динамики основано на абсолютном или относительном сравнении его уровней. Для характеристики интенсивности изменения во времени такими показателями будут:
1) абсолютный прирост,
2) темпы роста,
3) темпы прироста,
4) абсолютное значение одного процента прироста.
Показатели роста и прироста предназначены для характеристики изменения уровней ряда (yt), при этом сравниваемый уровень принято называть текущим (yi), а уровень, с которым производится сравнение, - базисным (y0). Показатели роста представляют собой отношение двух уровней, а прироста – их разность. Если эти показатели имеют вид относительных величин, их называют коэффициентами. Если они выражены в процентах – темпами.
Показатели ряда динамики могут быть цепными и базисными. В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели, при этом каждый последующий период сравнивается с периодом, принятым за базу.
Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях, при этом каждый последующий период сравнивается с предыдущим.
Расчет показателей динамики представлен в следующей таблице.
|
Показатель |
Базисный |
Цепной |
|
Абсолютный
прирост |
Yi-Y0 |
Yi-Yi-1 |
|
Коэффициент роста (Кр) |
Yi : Y0 |
Yi : Yi-1 |
|
Темп роста (Тр) |
(Yi : Y0)×100 |
(Yi : Yi-1)×100 |
|
Коэффициент прироста (Кпр )** |
|
|
|
Темп прироста (Тпр) |
|
|
|
Абсолютное значение одного процента прироста (А) |
|
|
*![]() **
**![]()
Рассмотрим пример расчета показателей ряда динамики (табл. 7.11) на основе имеющихся данных об объемах производства электроэнергии в РФ (источник: стат.сб. Регионы России, 2002 г.).
Абсолютное изменение уровней ряда измеряется показателем абсолютного прироста.
Цепные показатели прироста исчисляются так:
D2ц = y2 - y1 D3ц = y3 - y2 D 4ц = y4 - y3 . . . D iц = yi - yi-1
Базисные показатели прироста:
D2б = y2 - y1 D3б = y3 - y1 D4б = y4 - y1 . . . Diб = yi - y1
Абсолютный прирост характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени.
Абсолютные приросты с переменной базой (цепные) называют скоростью роста или первыми разностями.
Таблица 7.11
Динамика производства электроэнергии (млрд. кВт.ч)
|
Год |
Y |
Абсолютный прирост |
Темпы роста |
Темпы прироста, % |
|
Пункты |
|||
|
Dyц. = = yi – yi-1 |
Dyб = =yi – y1 |
Tр.ц = =(yi/yi-1)×100 |
Tр.б. = =( yi/y1)×100 |
Тпр.ц = =Тр.ц. – 100% |
Тпр.б. = =Тр.б. – 100% |
А% |
роста, % |
||
|
1995 |
14,9 |
- |
- |
- |
- |
- |
- |
- |
- |
|
1996 |
14,6 |
-0,3 |
-0,3 |
97,99 |
97,99 |
-2,01 |
-2,01 |
0,149 |
-2,01 |
|
1997 |
13,0 |
-1,6 |
-1,9 |
89,04 |
87,25 |
-10,96 |
-12,75 |
0,146 |
-10,74 |
|
1998 |
10,9 |
-2,1 |
-4,0 |
83,85 |
73,15 |
-16,15 |
-26,85 |
0,130 |
-14,1 |
|
1999 |
11,5 |
0,6 |
-3,4 |
105,50 |
77,18 |
5,5 |
-22,82 |
0,109 |
4,03 |
|
2000 |
10,7 |
-0,8 |
-4,2 |
93,04 |
71,81 |
-6,96 |
-28,19 |
0,115 |
-5,37 |
|
2001 |
15,7 |
5,0 |
0,8 |
146,73 |
105,369 |
46,73 |
5,37 |
0,107 |
33,559 |
|
|
å = 0,8 |
|
П = 1,05369 |
|
|
|
|
å =5,37 |
1995 – базисный год.
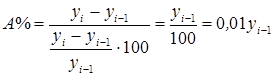 .
.
Цепные и базисные абсолютные приросты по данным приводимого примера показывают прирост (сокращение) производства электроэнергии и абсолютные изменения по сравнению с 1995 годом.
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени.
Для характеристики интенсивности, то есть относительного изменения уровня динамического ряда за какой-либо период времени исчисляют коэффициенты или темпы роста (снижения). Цепные коэффициенты роста исчисляются следующим образом:
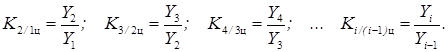
Цепные темпы роста будут иметь следующий вид:
Т2/1ц=(K2/1ц)100%, T3/2ц= (K3/2ц)100%, ….
Базисные же коэффициенты будут такими:
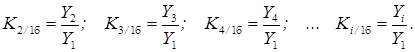
Базисные темпы роста:
T2/1б=(K2/1б)100%, T3/2б=(K3/2б)100% …
Они показывают во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если коэффициент больше 1) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы).
Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного коэффициента роста на предыдущий уровень равно соответствующему цепному коэффициенту роста.
Относительную оценку скорости изменения уровня ряда в единицу времени дают показатели коэффициентов (темпов) прироста. Темп прироста показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он представляет собой отношение абсолютного прироста к предыдущему или начальному (базисному) уровню. Цепной темп прироста:
Т пр.ц.=(åDyц/yi-1)100%;
T пр.б.=( Dyб/y1)100%.
Темп прироста можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием 1 из коэффициента роста.
При анализе динамики развития следует так же знать какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:
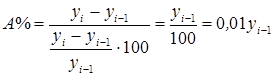
Абсолютное значение одного процента прироста показывает какое абсолютное значение скрывается за относительным показателем – одним процентом прироста.
Определение содержания одного процента прироста служит для правильной оценки успехов, достигнутых в истекшем периоде. Иной раз прирост в процентах выглядит очень внушительно. Но если проценты являются “пустыми”, то такой прирост не является настоящим успехом. Приведем такой пример. Допустим, число докторов наук в одном вузе за пять лет выросло с 2 до 4 человек, а во втором с 50 до 65. Если выразить прирост докторов наук в процентах, то он составит для первого вуза 100%, а для второго всего 30%. Однако это не значит, что второй вуз работал хуже: хотя его прирост в процентах оказался ниже, зато каждый процент прироста у него был более весомым, чем у первого.
В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают, так называемые, пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов.
В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным.
Пункты можно складывать и вычитать, ибо все они имеют одинаковое наполнение, так как исчислены по отношению к одной и той же базе, принятой за 100%. Этого нельзя сказать о процентах. Их база все время меняется.
Если показатель упал на 20 пунктов, а потом опять вырос на 20 пунктов, то он вернулся на прежний уровень. Когда подобное ожидают и от процентов, забывая о том, что они имеют у разных периодов разное наполнение, то совершают “ошибку перемены базы”. Эту ошибку, в частности, совершает тот, кто считает, что его зарплата вернется на прежний уровень, если она после падения на 20% в одном периоде вырастет на 20% в другом. Она станет у него в действительности меньше на 4%. ибо 0.8 ´1.2 = 0.96 или 96%.
| Предыдущая |