Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.

Предыдущая

Оглавление

Следующая

Глава 7. Статистическое изучение динамики общественных явлений

7.4. Средние показатели ряда динамики

Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины. Система средних показателей динамики включает следующие виды :

- средний уровень ряда,

- средний абсолютный прирост,

- средний темп роста,

- средний темп прироста.

Средний уровень ряда - это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.

Для интервальных рядов с равными периодами времени средний уровень Y рассчитывается по формуле простой арифметической:

 .             

Например, среднегодовой объем продукции трубопрокатного производства за семь лет с 1995 по 2001 гг. составил:

тыс. тонн.

Средний уровень моментного ряда исчисляется по формуле средней хронологической:

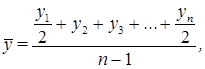
где  y₁   и  y_n  - начальный и конечный уровни  ряда,

y₂ , y₃  – промежуточные уровни; n – число уровней ряда, принимаемых  в расчет.

Например, средняя численность безработных за семь лет с 1995 по 2001 гг. (по состоянию на начало года) составила:

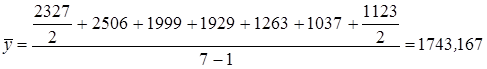тыс.чел.

Обращаем внимание на то, что начальный уровень ряда здесь показан как y₁,  а  не  y₀ .    

Чем больше промежуточных уровней участвует в расчете, тем точнее характеризуется средний уровень ряда. Когда же их нет, тогда средний уровень ряда исчисляют только по концам ряда.

Удовлетворительные результаты подсчета средней хронологической можно получить не всегда, а только для тех рядов, график которых близок к прямой, т.е. при наличии либо равномерного роста, либо равномерного падения.

Если же наблюдается ускоряющийся рост или ускоряющееся падение, и ряд на графике изображается кривой, то расчет среднего уровня только по концам ряда может дать ошибки, тем большие, чем больше кривизна кривой, изображающей этот ряд на графике. Уменьшить ошибки в таком случае можно с помощью следующей формулы:

,

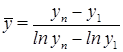где  lny_n  и lny₁ – натуральные логарифмы начального и конечного уровней ряда.

Проиллюстрируем использование этого приема. Допустим, ряд имеет такой вид:

Дата ( t )	1	2	3	4
Уровень ряда ( y )	10,0	12,7	16,8	22,0

На графике этот ряд будет изображаться кривой, все более круто забирающей вверх, что отражает ускоряющейся рост уровней этого ряда.

Средняя арифметическая, исчисленная по концам ряда, составит:

Средняя же, исчисленная по приводимой выше формуле, будет равна:

Это полностью совпадает с тем, что можно получить путем включения в расчет промежуточных уровней:

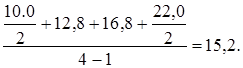
Конечно, в реальных условиях промежуточных уровней может и не оказаться, поэтому выбор лучшей формы расчета приходится делать не по близости к точной цифре, а исходя из предполагаемых тенденций изменения уровней ряда. Так, для ряда динамики численности населения можно предположить наличие изменений с неким одинаковым темпом роста, как условием применения упомянутой формулы. Для динамического ряда, характеризующего стоимость основных фондов предприятия на первое число каждого месяца расчет среднегодовой стоимости осуществляется только по формуле средней хронологической.   

Средний абсолютный прирост – обобщающий показатель скорости изменения уровней рядя во времени. По цепным данным об абсолютных приростах за ряд лет рассчитывается средний абсолютный прирост по формуле средней арифметической простой:

,

где  n – число цепных абсолютных приростов  в изучаемом периоде.

Используя расчетные данные таблицы 7.11 о цепных абсолютных приростах производства электроэнергии, исчислим средний абсолютный прирост:

  млрд кВт∙ч.

Можно вычислять средний абсолютный прирост и через накопленный (базисный) абсолютный прирост . Для случая равных интервалов применяется следующая формула:

,

где m – число уровней ряда динамики в изучаемом периоде, включая базисный.

Для нашего примера расчет будет следующим:

 млрд кВт∙ч.

Средний темп (коэффициент) роста или прироста является сводной обобщающей характеристикой интенсивности изменений уровней  временного ряда. Средний коэффициент роста исчисляется с помощью средней геометрической простой или взвешенной. Взвешенная используется  тогда, когда значения некоторых коэффициентов роста повторяются.

Средняя геометрическая простая  имеет следующую формулу :

 ,

где  К₁,К₂,К₃...К_n- цепные коэффициенты роста за  n периодов.

Поскольку произведение цепных коэффициентов дает базисный коэффициент роста, а базисный коэффициент можно получить делением конечного уровня на начальный, постольку приведенную выше формулу можно записать еще и так:

 .

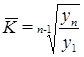Если бы начальный уровень был обозначен через y₀ , то корень надо было бы брать   n-ой степени, а  не степени  n-1.

Средний коэффициент роста для рассматриваемого примера  составит

 0,9677.

Следовательно, средний темп роста   здесь составил 96,77%, а средний темп прироста  равен –3,23%.

Средний темп прироста ни в коем случае нельзя исчислять по простой арифметической. Средний темп прироста (%) определяется по единственной методологии:

Согласно правилу мажорантности средних при использовании средней арифметической всегда получается завышенный результат по сравнению со средней геометрической. При коротких рядах это завышение может быть не очень заметным, но при длинных рядах оно может оказаться очень существенным.

Средняя геометрическая взвешенная имеет такой вид:

 .

Если два первых года ежегодный прирост был бы равен 20%, а последующие три года - 40%, то надо было бы воспользоваться последней формулой, которая в данном случае дала бы следующее значение среднегодового коэффициента роста

Последний расчет  вполне допустимо записать еще и так:

 .

В соответствии  с этим средняя геометрическая может  получить такой вид:

 ,

где  К_i – цепной коэффициент роста в i-том периоде,

w_i – вес i-того периода, исчисляемый как:

 .

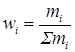Причем обязательно Sm_i =1.

В статистике для сравнения базисных темпов роста изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения

,

Где      - базисный темп первого ряда;

 - базисный темп второго ряда.

Период удвоения явления. В ряде случаев бывает полезно знать, за какое время уровень ряда удвоится при заданных темпах роста. Например, полезно знать, за какое время удвоится банковский вклад за счет начисляемых на него процентов или за какое время может удвоиться численность населения района, области, края или страны.^[6]

Расчет периода удвоения можно сделать следующим образом:

 ,

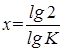где  х – период удвоения, К – заданный коэффициент роста.

Менее точно, но более просто расчет периода удвоения можно сделать и так:

  ,

где   d - cредний прирост в процентах.

Например, если население страны ежегодно увеличивается на 1%, то надо ожидать, что его численность удвоится за период длительностью:

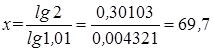года.

Если банковский вклад приносит 5% годовых, то он удвоится за период длительностью:

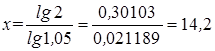  года.

Или, если применить более простой способ, через:

лет.

К сожалению, упрощенный способ расчета периода удвоения дает удовлетворительные результаты лишь при условии, что ежегодный прирост не превышает 30%. При более высоких темпах прироста он начинает сильно занижать период удвоения.

---

Предыдущая

Оглавление

Следующая