Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.

Предыдущая

Оглавление

Следующая

Глава 7. Статистическое изучение динамики общественных явлений

7.5. Методы анализа основной тенденции развития в рядах динамики

Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития. Для принятия эффективных управленческих решений на любом уровне необходимо обладать всей информацией об особенностях динамики изучаемого явления или процесса. Так, региональные власти должны знать, какова, например, динамика миграции населения области, республики или края, и чтобы управлять этим процессом необходимо иметь представление о том, увеличивается она или уменьшается в целом в рассматриваемый период времени. Это можно осуществить, применяя специальные методы анализа рядов динамики.

Изменения уровней временных рядов обуславливаются влиянием на изучаемое явление различных факторов, которые как правило, неоднородны по силе, направлению и времени их действия. Постоянно действующие факторы оказывают определяющее влияние и формируют в рядах динамики основную тенденцию развития. Воздействие других факторов проявляется периодически, что вызывает повторяемые во времени колебания уровней. Действия случайных (разовых) факторов отображается кратковременными изменениями уровней рядов динамики. 

Поэтому всякий ряд динамики теоретически может быть представлен в виде составляющих:

1) тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);

2) циклические (периодические) колебания, в том числе сезонные;

3) случайные колебания.

Под основной тенденцией развития (трендом) принято понимать достаточно плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Изучение тренда включает два основных этапа: на первом этапе ряд динамики проверяется на наличие тренда, а на втором производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Непосредственное выделение тренда может быть произведено методами укрупнения интервалов, скользящей средней или аналитического выравнивания.

1. Укрупнение интервалов. Один из наиболее простых приемов обнаружения общей тенденции развития. При этом первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Данные по месяцам можно преобразовать в данные по кварталам, квартальные данные преобразовать годовые и т.п. – эти величины получают путем простого суммирования. При суммировании уровней или при выведении средних по укрупненным интервалам отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более ясно обнаруживается действие основных факторов изменения уровней – основная тенденция.

Например, имеются данные об объемах продаж продукции птицефабрики (тыс. руб), причем при визуальном обзоре исходной информации, явная тенденция развития непосредственно не обнаруживается:

После укрупнения интервалов и преобразования ряда тенденция развития становится очевидной:

2. Скользящая средняя. При этом методе исходные уровни ряда заменяют средними величинами, которые получают, формируя укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал формируем, постепенно сдвигаясь от начального уровня динамического ряда на один уровень.

Так, по данным вышеприведенного примера произведем следующие вычисления:

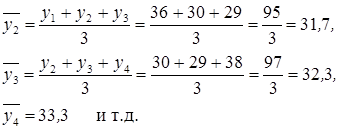
Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т. д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда с четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %.

Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда.

3. Аналитическое выравнивание. Основным содержанием данного метода является то, что основная тенденция развития изучаемого явления рассчитывается как функция времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех влияющих факторов, а отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или периодически. В результате приходят к трендовой модели:

Y_t = f(t) + e_t,

где f(t) – уровень, определяемый тенденцией развития;

e_t – случайное и циклическое отклонение от тенденции.

При этом определение теоретических, т.е. расчетных уровней временного ряда производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию изучаемого явления.

Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Вид функции выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. На данном этапе очень важно произвести качественный анализ изучаемого явления. Чтобы решить проблему подбора математической функции, по которой рассчитываются теоретические уровни тренда, необходимо изучить природу исследуемого явления или процесса. От правильности решения этой проблемы зависит обоснованность выводов о закономерностях тренда.  

Чаще всего при выравнивании используются следующие зависимости:

-  линейная Ŷ_t = a₀+a₁t;

-  параболическая Ŷ_t = a₀+a₁t+a₂t²;

-  экспоненциальные Ŷ_t = exp(a₀+a₁t) или Ŷ_t = exp(a₀+a₁t+a₂t² ).

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, - устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п.).

Наилучшим методом оценки параметров (a₀, a₁, a₂, ...) можно признать метод наименьших квадратов (МНК), который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:

∑(Ŷ_t –y_i)² →  min.

В качестве примера произведем выравнивание данных о производстве зерна в России по уравнению прямой (Ŷ_t  = a₀  +  a₁ t), используя два метода. Это метод наименьших квадратов и упрощенный метод выравнивания.

При использовании метода наименьших квадратов необходимо, чтобы сумма квадратов отклонений фактических данных от выравненных была наименьшей. Для нахождения параметров а₀ и а₁, строится система нормальных уравнений, которая имеет вид:

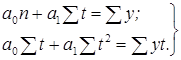
В рядах с равноотстоящими значениями можно выбрать упрощенный способ – способ условного отсчета времени ( t ), так, чтобы   Σt=0

Таблица исходных и расчетных данных

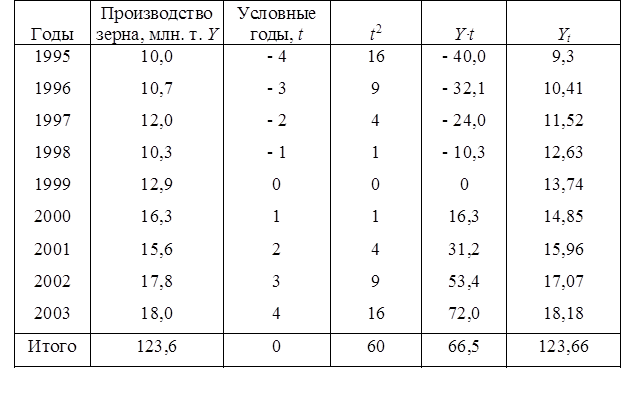
Следовательно,

 млн. т.;

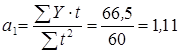 млн. т.

Таким образом, уравнение прямой примет вид:

Y_t =  13,74 + 1,11 t.

Подставив в это уравнение значение t, получим выровненные теоретические значения Y_t. Они показаны в последней колонке таблицы, причем общий объем производства зерна остался неизменным.

Пояснения к таблице.

Первые две колонки – ряд динамики, подвергаемый выравниванию, дополняется колонкой, в которой показана система отсчета времени "t". Причем эта система выбирается таким образом, чтобы t = 0.

Если число уровней ряда четное, то вместо нуля в центре мы поставили бы единицу с противоположными знаками у двух уровней, находящихся в середине ряда. Тогда разница между годами составляла бы две единицы времени и общий вид системы был бы таким (например, для ряда из 6 уровней):

Параметры a₀ и а₁ можно исчислить иначе с помощью определителей, построенных на основе системы нормальных уравнений:

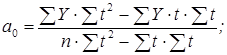
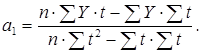
Приведенные формулы показывают, что для нахождения параметров a₀ и а₁ необходимо получить следующие значения:

 Обозначив годы t порядковыми номерами, определим эти величины и представим их значения в таблице.

Расчет параметров а₀ и а₁ с помощью определителей

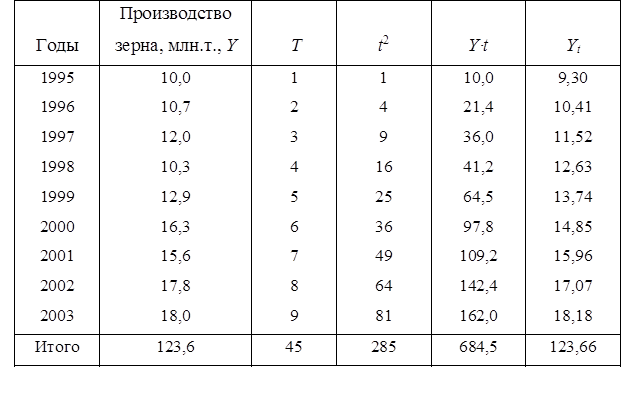
Далее определим параметры a₀ и а₁:

;

.

Следовательно,  Y = 8,19 + 1,66t.

Далее расчет аналогичен приведенному выше. Подставив в это уравнение значения t, получим выравненные теоретические значения Y_t.

После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.

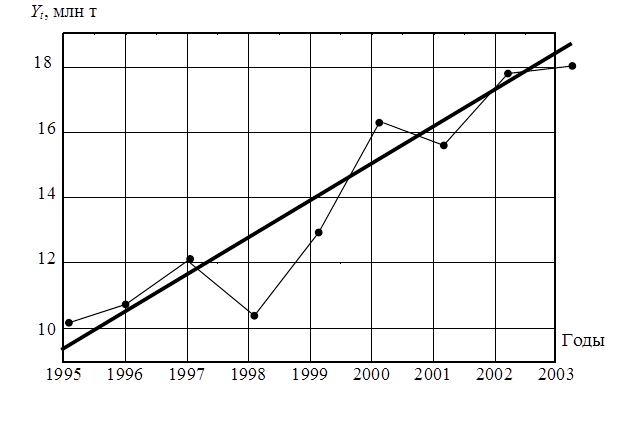
При решении некоторых вопросов приходится определять неизвестные промежуточные значения динамического ряда. Эта задача решается способом интерполяции. Интерполяция – это нахождение по ряду данных значений функции промежуточных ее значений, что, по сути, есть приближенное отражение сложившейся закономерности внутри определенного отрезка времени. Однако при прогнозировании процессов и явлений необходимо по ряду данных значений функции найти другие ее значения, находящиеся вне этого ряда. Для этих целей используется экстраполяция.

Экстраполяция заключается, по существу, в определении количественных характеристик для совокупностей и явлений, не подвергшихся наблюдению, путем распространения на них результатов, полученных из наблюдения над аналогичными совокупностями за прошедшее время, на будущее. Естественно, данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятные оценки будущего, поскольку в действительности тенденция развития не остается неизменной.

Предыдущая

Оглавление

Следующая