Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 8. Экономические индексы
8.5. Индексы переменного, постоянного состава и структурных сдвигов
Индексным методом можно воспользоваться для характеристики динамики средних показателей (уровней). Динамика среднего уровня находится под влиянием двух факторов: 1) изменение осредняемой величины, 2) изменение структуры явления или удельного веса численности отдельных групп в общем итоге (в общей численности). Например, средняя заработная плата работников предприятия может изменяться в результате изменения ставок заработной платы у отдельных категорий работников и в результате изменения удельного веса работников с различным уровнем оплаты труда.
Очень важно отметить следующее: при изучении динамики среднего показателя ставится задача показать роль каждого фактора в динамике этого показателя. т.е. измерить степень влияния в отдельности каждого фактора. С этой целью и строится система взаимосвязанных индексов: переменного состава, постоянного (фиксированного) состава (в постоянной структуре) и структурных сдвигов.
Индексы, исчисляемые путем сопоставления средних показателей, называются индексами переменного состава. Индексы переменного состава находятся под влиянием двух факторов, о которых говорилось выше.
В индексе постоянного (фиксированного) состава элиминируется, т.е. устраняется влияние второго структурного фактора и исчисляются они, таким образом, в постоянной структуре.
Индекс структурных сдвигов (или индекс структуры) позволяет измерить степень (меру) влияния структурных сдвигов. Исчисляются эти индексы по следующим формулам:
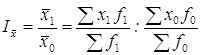
Зная,
что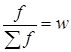 
, индекс можно представить в таком виде:
.
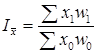Индексы постоянного (фиксированного) состава:
.
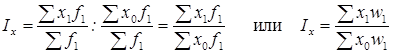Индексы структурных сдвигов:
.
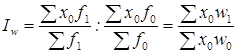Между приведенными индексами существует следующая взаимосвязь:
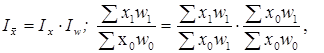
Следовательно,
.
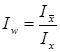Ряды индексов с постоянной и переменной базой сравнения (цепные и базисные). При изучении динамики общественных явлений за более или менее длительное время исчисляют не один, а ряд индексов. В тех случаях, когда сравниваемых периодов три и более возникает проблема выбора базы сравнения.
По базе сравнения различают цепные и базисные индексы. Цепными называются индексы, которые имеют переменную базу сравнения, а базисные индексы имеют постоянную базу сравнения.
Схема построения цепных индексов.
Исходные уровни: q1 q2 q3 q4
Цепные индексы: ip = 
; ip = 
; ip = 
;
Cхема построения базисных индексов.
Исходные уровни: q1 q2 q3 q4
базисные индексы:
iq = 
; iq = 
; iq = 
.
Между цепными и базисными индексами имеется определенная взаимосвязь, она заключается в следующем: произведение всех цепных индексов равно общему базисному индексу:
.
.
=
;
Отсюда следует: отношение каждого последующего базисного индекса к предыдущему базисному дает промежуточный цепной индекс:
: = ; : = ;
Взаимосвязь цепных индексов в индивидуальных проявляется всегда, а в сводных (общих) индексах только при условии постоянства весов (или соизмерителей).
Возьмем ряд цепных индексов с постоянными весами (р1):
Iq =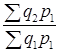 
; Iq = 
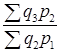; Iq =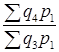 
Если перемножить эти индексы, то получим общий базисный индекс:
.
.=
;
Этому требованию не отвечают индексы с переменными весами:
Iq = 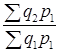; Iq = 
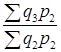; Iq = 
.
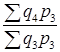Ряды индексов с постоянными и переменными весами. Два и более индексов с одинаковыми по содержанию и во времени весами образуют ряд индексов с постоянным весами или соизмерителями:
Iq = 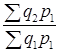; Iq = 
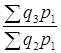; Iq = .
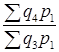Два и более индексов с одинаковыми по содержанию, но различными во времени весами или соизмерителями называются рядом индексов с переменными весами или соизмерителями:
Iq = 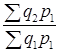; Iq = 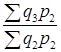; Iq =.
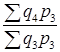В статистической практике ежегодные индексы объема промышленной продукции вычисляются как индексы с постоянными соизмерителями или весами, т.к. продукция оценивается в сопоставимых ценах. Ежегодные индексы физического объема продукции в торговле вычисляются как индексы с переменными весами или соизмерителями.
| Предыдущая |
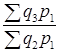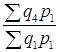