Л.И. Ниворожкина, Т.В. Чернова
Теория статистики (с задачами и примерами по региональной экономике)
Учебное пособие. – Ростов н/Д: «Мини Тайп», «Феникс», 2005. – 220 с.
| Предыдущая |
Глава 8. Экономические индексы
8.6. Индексный метод анализа факторов динамики
Многие статистические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи, представленной чаще всего в виде произведения. Связь между экономическими показателями находит свое отражение и во взаимосвязи характеризующих их индексов.
В общем случае, если z = yx, то Iz = IyIx, а если z = y/x, то и Iz = Iy / Ix.
Поэтому многие, связанные между собой экономические показатели, образуют индексные системы.
Система взаимосвязанных индексов дает возможность применять индексный метод для изучения взаимосвязи общественных явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга) на изменение сложного явления
В отечественной статистике практике принята следующая практика факторного анализа. Если результативный показатель можно представить как произведение объемного и качественного показателя, то, определяя влияние объемного фактора на изменение результативного показателя, качественный фактор фиксируют на уровне базисного периода. Если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода.
Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах промышленности) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости (товарооборота в фактических ценах). Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарооборота в фактических ценах):
или 
.
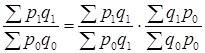Таким образом, произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах), т.е. индексы образуют индексную систему из трех индексов.
Если, например, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 20% (Ip,= 1,20), а физический объем товарооборота в фиксированных ценах снизился на 5% (Iq = 0,95), то можно определить изменение объема товарооборота в фактических ценах:
Ipq = Ip . Iq = 1,20 . 0,95 = 1,14 или 114%.
Таким образом, при снижении физического объема товарооборота на 5%, товарооборот в фактических ценах в отчетном периоде по сравнению с базисным вырос на 14% вследствие роста цен на единицу товара в среднем на 20%.
Аналогично можно найти взаимосвязь между индексами затрат на производство продукции, себестоимости и физического объема продукции:
Izq = Iz . Iq.
Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих Т и заработной платы f:
IF = IT . If.
К числу взаимосвязанных индексов относятся и индексы переменного состава, индексы постоянного состава и индексы структурных сдвигов. В этой системе динамика среднего показателя (индекса переменного состава) выступает как произведение двух индексов: индекса среднего показателя в неизменной структуре (индекс постоянного состава) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов):
.
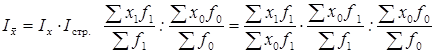Индексная система позволяет определить влияние отдельных факторов на формирование уровня результативного показателя, т.е. по двум известным значениям индексов найти значение третьего – неизвестное. Например, известно, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным выросли на 15% (Izq = 1,15) и одновременно уровень себестоимости единицы продукции снизился на 4% (Iz = 0,96), то можно определить, что физический объем продукции вырос на 20%:
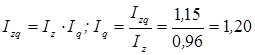или 120%.
Рассмотренные системы являются двухфакторными (результативный признак связан с двумя факторами), но общий признак может зависеть от трех, четырех и более факторов, т.е. связь может трех-, четырехфакторная и т.д.
Поэтому общие индексы могут быть разложены также на три, четыре и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности.
Обозначим факторные признаки a, b, c, тогда система взаимосвязанных индексов будет иметь следующий вид:
.
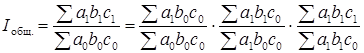Аналогично строится система взаимосвязанных индексов при четырехфакторной связи и т.д.
| Предыдущая |