А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.

Предыдущая

Оглавление

Следующая

Глава 2. Методы и подходы к формированию (организации) долгосрочных виртуальных предприятий

2.1. Формирования «ядра» бизнеса долгосрочного виртуального предприятия

Как было отмечено ранее, у участников сети долгосрочного виртуального предприятия, как правило, нет постоянных подкрепленных обязательствами связей с центром и другими агентами (см. 1.3). Достаточно устойчивые связи возникают только на момент выполнение определенного рыночного заказа или задачи при принятии участником  на себя определенных обязательств. Рыночные же заказы могут быть разнообразны, спонтанны, неравномерно распределены во времени.

В таких условиях, в первую очередь, необходимо формирование «ядра» долгосрочного виртуального предприятия понимаемое как определенный состав участников, обладающих компетенциями (ресурсами, знаниями и умениями) для поиска и исполнения основного потока рыночных заказов и задач предприятия в соответствии с предназначением, направлением и сферой деятельности предприятия.

Ядро на базе существующей динамической сети предполагается формировать следующим образом:

1. Определение рыночной возможности, формирование бизнес-идеи как направления и сферы деятельности виртуального предприятия;

2. Определение минимума ключевых компетенций для осуществления деятельности по выбранному направлению и сфере деятельности;

3. Определение состава, возможностей и компетенций участников динамической сети;

4. Построение матриц возможностей участников сети в соответствии с требуемыми ключевыми компетенциями для осуществления деятельности долгосрочного виртуального предприятия.

5. Отбор и объединение участников сети, имеющих наибольшее совпадение возможностей с требуемыми ключевыми компетенциями.

6. Отбор предприятий для формирования «ядра» бизнеса на основе формирования матриц связности.

При отсутствии устойчивых связей между участниками виртуального предприятия либо при первоначальной организации виртуального предприятия, исходя только из направления деятельности (сферы бизнеса), необходимо определение наиболее значимых потенциальных партнеров, которых необходимо привлечь в сеть.

Для первоначального отбора потенциальных партнеров можно воспользоваться матрицами связанности, в которых отражается связь компетенций потенциальных партнеров с требуемыми компетенциями.

Этапы построения матриц связанности можно представить следующим образом:

1.  Определение множества требуемых компетенций предприятия, на базе которого планируется объединить другие, {К_i}, где i=1..n, n - количество компетенций;

2.  Определение множества компетенций каждого потенциального k-го партнера {P_j}, где j=1..m, m - количество компетенций каждого потенциального партнера.

3.  Составление матриц связанности с элементами {a_ij}, где отражена связь i-ой требуемой компетенции с j-ой компетенцией k-го партнера, 0 - отсутствие связи.

4.  Для каждого потенциального партнера суммируется количество связей: S_kj = S_I a_ij

5.  Ранжирование партнеров по S_i.

Матрицы связанности позволяют определить максимально соответствующих предъявляемым компетенциям потенциальных партнеров.

Для уточнения «ядра» с учетом взаимосвязанности всех потенциальных партнеров друг с другом предлагается применить метод симплициального комплекса.

В то же время важной оценкой является оценка «ядра» с точки зрения наибольшего числа компетенций объединяемых партнеров.

Для получения этой оценки предлагается исследовать возможность применения закономерностей информационных потоков, исследованных в теории научно-технической информации.

Формирование «ядра» бизнеса на основе использования закономерностей документальных информационных потоков (ДИП)

При формировании «ядра» бизнеса виртуального предприятия возможно воспользоваться закономерностями документальных информационных потоков, а именно закономерностями «концентрации и рассеяния».  Рассмотрим их подробнее.

Закономерность (закон Брэдфорда), установленная эмпирически английским химиком и библиографом С.Бредфордом в 1948 г. [94] заключается в том, что если научные журналы расположить в порядке убывания числа статей по конкретной проблеме, то журналы можно разбить на три зоны таким образом, чтобы количество статей в каждой зоне по заданной теме было одинаковым.

При этом в первую зону, названной Брэдфордом зоной ядра, входят профильные журналы, непосредственно посвященные рассматриваемой тематике. Количество журналов в зоне ядра невелико.

Вторую зону образуют журналы, частично посвященные заданной области, причем их число существенно возрастает по сравнению с числом журналов в ядре.

Третья зона - самая большая по количеству изданий - объединяет журналы, количество которых весьма далека от рассматриваемой предметной области.

При равном числе публикаций в каждой зоне число источников резко возрастает при переходе от одной зоны к другой. Брэдфорд установил, что число наименований журналов в третьей зоне примерно во столько раз больше, чем во второй зоне, во сколько раз число наименований журналов во второй зоне больше, чем в ядре:

где Р_1, Р_2, Р₃ - число наименований журналов в 1-й, 2-й и 3-й зонах соответственно.

Б. Викери уточнил модель С. Брэдфода [94–97, 108]. Он выяснил, что журналы, проранжированные в порядке уменьшения в них статей по конкретному вопросу, можно разбить не на три зоны, а на любое число зон. Основной смысл закономерности Викери (рис. 2.2): если периодические издания расположить в порядке уменьшения в них количества статей по конкретному запросу, то в полученном списке можно выделить ряд зон, каждая из которых содержит одинаковое количество статей. При этом число журналов в первой зоне и нарастающее их число в последующих зонах соотносятся следующим образом:

Т_x: Т_2x: Т_3х: Т_4х:... = 1: а : а²: а³: ...,

где х - количество статей в каждой зоне; Т_х, - количество журналов, содержащих х статей; T_2x, T_3x, Т_4х, ... - количество журналов, содержащих 2х Зх, 4х и т.д. статей соответственно.

Часто этот закон называют законом Брэдфорда в толковании Викери.

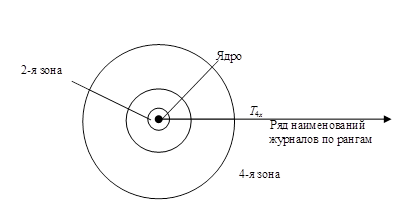
Рис. 2.2. Иллюстрация закона Брэдфорда в толковании Викери

В работах [53, 90, 95, 96] было показано, что количественные закономерности строения (ДИП) могут быть выражены как посредством количественных параметров ранговых распределений (закономерность Ципфа), так и посредством параметров упорядоченных потоков элементов ДИП (закономерность Брэдфорда–Викери), т.е. что эти закономерности отображают одно феноменологическое явление.

Смысловой анализ эмпирических данных строения подсистем ДИП,  проведенный в работах В.И.Горьковой и ее учеников [24-28 и др.] позволил зафиксировать наличие специфических функциональных свойств различных частотных зон ранговых распределений и упорядоченных потоков. Научные журналы, наиболее продуктивные по числу научных статей для соответствующего тематического раздела, сосредоточены в зоне рангового распределения, где частоты появления наименований элементов наибольшие, т.е. в ядре рангового распределения.

Структурное подмножества ядра рангового распределения состоит из профильных научных журналов, которые составляют ~10% от всех наименований журналов, содержащих публикации по данному тематическому разделу; при этом в научных журналах, входящих в ядро рангового распределения, содержится 50–60%  всех публикаций по данной тематике [25, 53, 95, 96].

Тематическое содержание профильных журналов ядра рангового распределения определяет тематические признаки данного упорядоченного потока.

Для ядерного подмножества терминов рангового распределения характерно вхождение в него заглавных понятий, тематическое содержание которых определяет классификатор данного тематического раздела. В зону ядра рангового распределения авторов публикаций входят имена исследователей, которым принадлежат основополагающие положения тематического раздела [25].

На основе исследования этих специфических особенностей ядра В.И. Горьковой был сделан вывод о том, что явление образования ядра рангового распределения системы ДИП можно трактовать как свойство системы ДИП концентрировать в ядре рангового распределения логическую информацию, определяющую основные понятия предметной области, объектов и методов исследования соответствующей отрасли науки (техники), научной дисциплины.

Явление образования ядра Горькова рассматривает как организацию высокого уровня, когда между элементами подмножества ядра существуют взаимосвязи, играющие более важную роль, чем связи между элементами других подмножеств. Элементы ядра выступают в роли «организаторов» подсистемы ДИП в конкретной отрасти науки или научной дисциплине, т.е. выполняют функции организующих отношений системы ДИП. Наименования элементов зоны ядра ДИП определяют условия включения элементов всех других частотных зон ранговых распределений в данную упорядоченную совокупность.

Одновременно с явлением образования ядра рангового распределения элементов ДИП по тематическому разделу наблюдается рассеяние элементов.

Так, если ядро содержит ~10% от всех наименований элементов ДИП, что составляет 50–60 % упорядоченного потока подсистем ДИП, то в зоне рассеяния при наименовании элементов ~90% сосредоточено всего 40–50 % упорядоченного потока документов.

Зона рассеяния рангового распределения определяет структуру связи подсистем ДИП различных отраслей науки (техники) или научных дисциплин, взаимно обогащающих друг друга семантической информацией.

Следует отметить, что рассмотренные функциональные свойства двух зон рангового распределения и упорядоченного потока огрубленно трактуют функциональные свойства ранговых распределения. В зоне рассеяния можно выделить третье структурное подмножество элементов с малой частотой появления, обладающее специфическими свойствами. В дальнейшем, видимо, возможна и более детальная структуризации зоны рассеяния. 

Рассмотренное феноменологическое явление концентрации и рассеяния элементов ДИП было названо закономерностью концентрации – рассеяния.

 Действие закономерности концентрации – рассеяния основано на том, что упорядоченное множество элементов ДИП имеет два  структурно-функциональных свойства.

Во-первых, концентрировать подмножества ядерных элементов, функция которых состоит в том, чтобы:

а) сосредотачивать логическую информацию, определяющую основные предметы, объекты и методы исследований в отрасли науки;

б)  выполнять роль «организующих отношений».

Во-вторых, рассеивать подмножество элементов, функция которых состоит  в том, чтобы:

а) определять структурные связи подсистем ДИП различных отраслей науки и научных дисциплин, обогащающих друг друга семантической  информацией;

б) обеспечивать определенную целостность всей подсистемы ДИП.

Закономерности концентрации – рассеяния позволяет использовать параметры аппроксимирующих функций, описывающих ранговые распределения и упорядоченные потоки в качестве параметров, определяющих функциональные свойства упорядоченных совокупностей элементов ДИП.

Следует еще раз обратить внимание на тот факт, что численные меры упорядоченности строения ДИП, определяемые статистическими методами только тогда могут использоваться в практике научно-информационной деятельности, когда они сочетаются с методами исследования функциональных свойств упорядоченных совокупностей ДИП.

Закономерности ДИП используются при комплектовании фондов и создании системы справочно-информационного обслуживания в библиотеках и отделах научно-технической информации, при создании и совершенствовании классификационных систем (отборе классификационных понятий), при аналитико-синтетической обработке текстов.

Можно предположить, что подобная закономерность характерна и для видов бизнеса,  направлений деятельности предприятий и распределения компетенций по предприятиям.

Согласно этим закономерностям можно сформировать группы предприятий, которые обладают требуемыми компетенциями для ведения определенного бизнеса, соотносящиеся следующим образом:

Т_х : Т_2x : Т_3х : Т_4х : ... = 1 : а² : а³ : а⁴ : ...,

где х - количество компетенций в каждой зоне; Т_х, - количество предприятий, содержащих х компетенций; Т_x, Т_3x, Т_4х, ... - количество предприятий, содержащих 2х, Зх, 4х и т.д. компетенций соответственно;

Упорядочение потенциальных партнеров на основе применения метода симплициального комплекса

Эффективного отбор и объединение потенциальных партнеров могут достигаться путем выявления потенциальных партнеров, уже имеющих связи между собой. Для этого воспользуемся подходом к анализу связности в системах методом симплициального комплекса, базирующегося на идеях работ Дж. Касти [37].

Для того, чтобы наглядно изучить связность структуры, необходимо рассмотреть понятие комплекса. Симплициальный комплекс - это естественное математическое обобщение понятия планарного графа, отражающего многомерную природу бинарного отношения. Поскольку симплициальный комплекс, по существу, не что иное, как семейство симплексов, соединенных посредством общих граней, то естественной характеристикой связности могла бы служить размерность грани, общей двум симплексам. Однако, нас интересует комплекс в целом, поэтому более целесообразно использовать понятие цепь связи, отражающее тот факт, что два симплекса могут не иметь общей грани, но могут быть связаны при помощи последовательности промежуточных симплексов. С учетом соображения размерности понятие q-связности может быть сформулировано следующим образом.

Даны два симплекса s_i и s_j комплекса К соединены цепью q-связи, если существует последовательность симплексов {s_ai}ⁿ_i=1 в К, такая, что s_a1-грань s_i., s_an- грань s_j, s_ai и s_ai+1 обладают общей гранью размерности b для i = l,2,..., n - l, q=min {i, b₁ b₂, …, ,b_n, j} [37].

Нижний индекс симплекса соответствует его геометрической размерности, например dim s_s= s.

Таким образом, задача изучения глобальной структуры связности комплекса К сводится к рассмотрению классов q-эквива-лентности. Для каждого значения размерности q = 0,l,...,dim К можно определить число различных классов эквивалентности Q_q. Назовем эту операцию q-анализом комплекса К, а вектор    Q= (Q_dimK> …>Q,Q₀)- первым структурным вектором комплекса.

Несмотря на то что q-анализ оказывается довольно эффективным при изучении глобальной связности структуры, тем не менее он не дает необходимой информации о том, как каждый отдельный симплекс входит в весь комплекс. Поскольку, индивидуальные свойства симплексов могут оказаться весьма существенными в рассматриваемой проблеме, важно уметь определять степень интегрированности каждого отдельного симплекса в структуре всего комплекса. Для этой цели  в [37] введено понятие эксцентриситет.

Эксцентриситет симплекса  задается следующей формулой:

,  где q' -размерность симплекса s, a q" - наибольшее значение q, при котором s становиться связанным с каким-либо другим симплексом из К.

Проведем анализ взаимосвязи потенциальных партнеров, необходимых для реализации конкретной бизнес-идеи в рамках виртуального предприятия, методом симплициального комплекса.

1. В качестве исследуемой системы рассмотрим граф взаимосвязи потенциальных партнеров, в котором дуга между двумя вершинами указывает на существование связи между соответствующими потенциальными партнерами. Полученный граф представим в виде матрицы Е системных взаимосвязей, (i,j)-й элемент которой равен 1, если предприятия i и j связаны, и равен 0 в противном случае (табл. 2.2).

Таблица 2.2.

	П1	П2	...	Пk	...	Пn
П1	0	1		1		0
П2	1	0		0		0
...	1	0		1		1
Пn	0	1		0		0
...
Пn	0	1		1		0

2.  После формирования матрицы инциденций проводится оценка связности с применением q-анализа.

3.  Завершающим этапом анализа матрицы инциденций является вычисление эксцентриситета    

                               ,

где q' - размерность симплекса s, a q" - наибольшее значение q, при котором s становиться связанным с каким-либо другим симплексом из К.

На основе оценки эксцентриситета можно упорядочить партнеров по степени интеграции одного предприятия с другими, что позволяет осуществлять отбор предприятий с определенной взаимосвязанностью друг с другом. Причем, на практике центр виртуального предприятия в зависимости от стратегии и целей может отбирать не максимально взаимосвязанных партнеров, а имеющих наименьшую связь.

Предыдущая

Оглавление

Следующая