А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.
| Предыдущая |
Глава 1. Виртуальные предприятия как новая организационная форма управления
1.4. Задачи и модели управления виртуальным предприятиям как организационной системой
Общие задачи управления организационными системами условно можно разбить на пять классов [10]:
1. Задачи формирование состава и структуры системы, включая "задачи о назначении" и распределении функций.
2. Задачи оценки эффективности деятельности элементов системы, то есть выбора критериев оценки, шкал и процедур: получения и агрегирования информации, выбора вариантов и др.
3. Задачи определение процедуры распределения ресурсов (материальных, финансовых, кадровых, и др.) в управляемой системе, имея заданную структуру, систему сбора и обработки информации и т.п.
4. Задачи обеспечения координации и согласования интересов, включая задачи стимулирования и мотивации.
5. Задачи контроля и оперативного управления, т.е. отслеживание функционирования управляемой системы в реальном времени и внесение корректив в случае отклонения ее показателей от запланированных.
Для решения этих задач разработано множество математических моделей управления организационными системами, которые основываются на аппарате и результатах ряда теорий: теории принятия решений [18, 23, 29, 60, 66, 89 и др.]; математической экономики [7, 8, 33, 35, 61 и др.]; теории игр [18, 23, 29, 56, 98], в том числе – деловых и имитационных игр [3, 12, 13, 93]; теории управления проектами (в том числе – организационными проектами или проектами реформирования или реструктуризации [5, 6, 13]), включая как качественные [16, 62, 87], так и формальные подходы [4, 10, 14, 19, 54].
Математические модели управления основываются на следующей основной идее оптимизации функционирования организационной системы. Предполагается, что известны: параметры, описывающие состояние управляемой системы и внешних условий ее функционирования (окружающей среды); зависимость состояния системы от управляющих воздействий; множество допустимых управляющих воздействий; критерий эффективности функционирования системы (позволяющий сравнивать по эффективности любые ее состояния).
При этом критерием эффективности управления является значение критерия эффективности состояния системы, в котором она оказалась под влиянием этого управления. Тогда задача оптимизации заключается в поиске допустимого управляющего воздействия, имеющего максимальную эффективность, то есть приводящего систему в наиболее эффективное состояние. Общая схема структуры системы управления элементом организационной системы приведена на рис. 1.4.
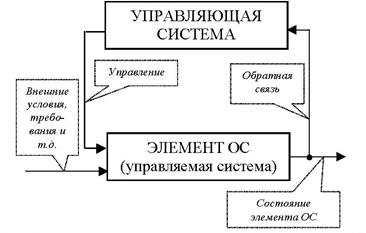
Рис. 1.4. Общая схема структуры системы управления элементом организационной системы
Выбирая соответствующие признаки классификации, можно выделить следующие виды управления:
· административное (институциональное, командное) и/или мотивационное управление (управление, побуждающее управляемых субъектов к совершению требуемых действий);
· проектное управление (управление в динамике – изменениями в системе, инновационной деятельностью и т.д.) и процессное управление (управление функционированием – «в статике» – регулярной, повторяющейся деятельностью при неизменных внешних условиях).
Модель организационной системы определяется заданием [11]: состава (участников, то есть элементов системы); структуры (совокупности информационных, управляющих, технологических и других связей между участниками); множеств допустимых стратегий участников, отражающих, в том числе, институциональные, технологические и другие ограничения их совместной деятельности; целевых функций участников, отражающих их предпочтения и интересы; информированности – той информации, которой обладают участники на момент принятия решений о выбираемых стратегиях; порядка функционирования: последовательности получения информации и выбора стратегий участниками системы.
Следовательно, признаком системы классификаций механизмов управления (процедур принятия управленческих решений) является предмет управления – изменяемая в процессе и результате управления компонента системы.
По признаку «предмет управления» можно выделить: управление составом [30, 36]; управление структурой [70, 72]; институциональное управление (управление «допустимыми множествами»); мотивационное управление [68, 71] (управление предпочтениями и интересами); информационное управление (управление информацией, которой обладают участники системы на момент принятия решений) [69]; управление порядком функционирования (управление последовательностью получения информации и выбора стратегий участниками системы), которое обычно рассматривают как управление структурой [72].
Простейшая (базовая) модель организационной системы включает одного управляемого субъекта – агента – и одного управляющего органа – центра, которые принимают решения однократно и в условиях полной информированности.
Расширениями базовой модели являются: динамические организационные системы (в которых участники принимают решения многократно) [73]; многоагентные (многоэлементные) системы (в которых имеется несколько агентов, принимающих решения одновременно и независимо) [68]; многоуровневые системы (иерархическую структура имеющая более двух уровней) [70, 72]; системы с распределенным контролем (в которых имеется несколько центров, осуществляющих управление одними и теми же агентами) [30, 36]; системы с неопределенностью (в которых участники не полностью информированы о существенных параметрах) [67, 68]; системы с ограничениями совместной деятельности (в которых существуют глобальные ограничения на совместный выбор агентами своих действий) [69]; системы с коалиционным поведением участников [30]; системы с сообщением информации (в которых одним из действий агентов является сообщение информации друг другу и/или центру) [67, 73, 76].
Ключевыми для теории управления организационными системами понятием являются понятие механизма функционирования системы – совокупности законов, правил и процедур, регламентирующих взаимодействие участников системы; и понятие механизма управления - совокупности процедур принятия управленческих решений. В рамках настоящего исследования наиболее важны модели формирования и управления сетью партнеров как для эффективного функционирования всего долгосрочного виртуального предприятия, так и выполнения отдельных проектов.
В этой связи, наибольший интерес из работ по теории организационных систем представляет работа [72], в которой исследованы теоретико-игровые модели формирования (синтеза) сетевых структур. В работе показано, что структура определяется типом иерархической игры, разыгрываемой участниками системы. Такой подход позволяет анализировать сетевые структуры, в которых потенциально существуют связи между всеми участниками, некоторые из которых актуализируются, порождая на время решения стоящей перед системой задачи определенную иерархию. Значительное внимание уделено частным случаям: линейные системы, веерные структуры, систем с побочными платежами, задачи управления проектами в сетевых структурах.
В основном задачи структурного синтеза исследованы в рамках моделей, в которых предпочтения агентов описываются «абстрактными» целевыми функциями, а структуре соответствует разделение агентов на множества, упорядоченные в соответствии с последовательностью выбора стратегий [72].
В работе [72], также отмечается, что имеющийся на сегодняшний день опыт анализа специфики того или иного механизма управления в различных организационных структурах, включая сетевые, ограничивается задачами идеального агрегирования и произвольной децентрализации механизмов управления фиксированным набором агентов при условии, что объединение агентов в группы и управление этими группами производится внешними центрами. В то же время, в задачах структурного синтеза (формирования структуры) назначение управляющих органов возможно производить из числа агентов.
Из механизмов управления в сетевых структурах, к которым относятся и кооперационные сети предприятий, приведены в [72] модели формирования мультиагентной системы (модели размещения центром заказа на нескольких предприятиях) и модели внутренних цен.
Задача размещения центром заказа на 
предприятиях
формулируется следующим образом: представители
предприятий - агенты - взаимодействуют между собой и с центром с
целью получения заказа на производство. Цель центра - размещение заказа с минимальными затратами 
,
цель каждого из агентов - максимизация
прибыли, определяемой как разность между вознаграждением, выплачиваемым
центром, и собственными затратами. При этом известны 
- удельные переменные издержки 
-го
предприятия по производству 
-го вида продукции, 
- постоянные издержки i-го
предприятия, 
- объем
выпуска j-го продукта на i-ом предприятии, 
- суммарное количество продукции j-го вида, требуемое в заказе, 
- заказ выпуска j-го продукта i-му предприятию, 
- цена, установленная заказчиком (центром)
на единицу продукции j-го вида, 
.
Предполагается сначала, что
центр имеет полную и достоверную информацию о параметрах 
агентов и заинтересован в том, чтобы все
агенты работали безубыточно. Последнее условие может иметь место в случае,
когда агенты представляют собой, например, подразделения корпорации, холдинга
или вертикально интегрированной компании, а выступающее в роли центра руководство
холдинга или компании несет ответственность за деятельность всех подразделений.
Условие безубыточности тогда записывается в виде:
. (1.1)
Задача центра заключается в
нахождении цен 
и заказов ,
минимизирующих при ограничениях (1.1) и 
и является стандартной задачей математического
программирования.
Просуммируем условия
безубыточности по всем предприятиям: 
. В левой части
неравенства стоит целевая функция центра, в правой - суммарные затраты агентов. Поэтому
требование обеспечения безубыточности
деятельности агентов в определенном смысле эквивалентно стремлению центра к
минимизации их суммарных затрат. При этом, во-первых, не для всякого вектора 
заказов найдутся цены 
, обеспечивающие безубыточность
деятельности всех агентов, а, во-вторых, рассмотренная модель отражает
достаточно узкий круг реальных явлений.
Поясним последнее утверждение. Рассмотренная модель описывает, фактически, задачу требование учета центром безубыточности агентов в условиях полной информированности. Последнее означает, что центру известны все основные параметры агентов, а последние ведут себя пассивно, выбирая действия, совпадающие с назначенными центром планами. В практической деятельности более распространена ситуация, в которой центр является заказчиком и не интересуется благосостоянием агентов, которые сами предлагают условия, на которых они готовы взяться за выполнение заказа.
В этом случае, предполагается, что постоянные издержки агентов могут быть отнесены к конкретным производимым продуктам, а переменные издержки описываются квадратичной функцией затрат типа Кобба-Дугласа, то есть функции затрат имеют вид [125]:
.
Тогда в предположении, что
агенты самостоятельно выбирают объемы выпуска при заданных внешних
(устанавливаемых центром) ценах, можно вычислить лимитные цены (минимальные
цены, обеспечивающие безубыточность производства) каждого агента по каждому
виду продукции: 
и соответствующие точки
безубыточности 
.
Следовательно, при цене - i-ый агент будет производить продукцию в объеме 
, только если 
.Задача
центра при этом может быть записана в виде:
,
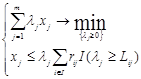где 
- функция-индикатор неотрицательности
своего аргумента. Приведенная задача центра может быть декомпозирована на m независимых задач определения цен по каждому виду продукции
(для фиксированного продукта индекс, обозначающий номер этого продукта, будет
опускаться):
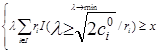
При известных параметрах агентов решение данной задачи элементарно: центру следует упорядочить агентов в порядке возрастания лимитных цен и распределять задания между ним до тех пор, пока не будет распределен весь заказ.
Итак, пусть 
- упорядочение агентов. Определим 
. Тогда
в оптимальном (то есть минимизирующем цену) решении
, а
объем выпуска равен
. Таким образом, получается
квазиаукционное решение - заказ получат агенты, имеющие минимальные лимитные
цены. Однако, для того, чтобы найти это аукционное решение центр должен знать
истинные значения лимитных цен, что имеет место не во всех возникающих на
практике случаях, поэтому рассмотрим, что произойдет, если лимитные цены неизвестны
центру и он вычисляет их на основании сообщаемой агентами информации.
Предположим, что центру
неизвестны эффективности 
деятельности агентов.
Обозначим 
- сообщения
агентов об эффективности собственной деятельности.
На основании сообщений центр
может вычислить 
соответственно лимитную цену и
точку безубыточности каждого агента.
Таким образом, возникает игра агентов, в которой их выигрыши зависят от сообщаемой информации. Отметим, что, так как вычисляемая центром лимитная цена каждого агента зависит только от его собственных сообщений, то можно условно считать, что он сообщает непосредственно оценку лимитной цены, а игра возникает при подстановке этих оценок в принцип принятия центром решений о назначаемой цене [72].
Легко видеть, что равновесием
Нэша игры агентов является сообщение ими достоверной информации. Этот факт
обусловлен тем, что центр использует одинаковую для всех агентов цену. Если бы
внешние цены для разных агентов были различны, то получилось бы классическое
аукционное решение игры с сообщением информации, в котором первые 
агентов сообщили бы одинаковые
оценки, а именно - лимитную цену 
.
При использовании описанного
механизма центр «переплачивает» агентам (сверх минимально необходимой)
следующую величину: 
. При этом очевидно, центр
не может размещать заказ произвольного размера - существуют значений заказов, которые могут быть
выполнены агентами по лимитным ценам (назначение внешней цены в промежутке между
лимитными ценами агентов не изменит их суммарный объем выпуска, а только
увеличит расходы центра): 
. Соответствующие
затраты 
центра на размещение заказа равны 
.
В [72] также приводятся модели
объединения агентов для обеспечения суммарного объем выпуска 
, который может интерпретироваться
как внешний заказ, на основе внутренних цен. Учитываются суммарная полезность
для каждого агента, центра и стоимость заказа.
В исследуемых моделях рассматриваются только ситуации, когда заказ однороден, может быть разбит на части и размещен на разных предприятиях, что характерно для производственных предприятий, когда выпускается одинаковая продукция. Ситуации, когда заказ включает множество различных услуг (задач), которые могут быть взаимосвязаны и распределены во времени, не рассматриваются. А такие задачи наиболее типичны для рынка услуг (консалтинговые услуги, строительство, информационные услуги и др.). Следовательно, далее в диссертационном исследовании основное внимание необходимо уделить моделям распределения различных заказов.
Необходимо отметить, что наиболее распространенными методами исследования взаимодействия и переговорных процессов в теории управления организационными системами являются методы теории полезности и теории игр, в частности, известные модели и условия оптимальности, выраженные в виде принципов равновесия.
Равновесие по Парето применяется для сильно централизованных систем, подсистемы которых имеют широкие возможности обмена информацией о принимаемых решениях, а равновесие по Нэшу характеризует децентрализованные системы. Эти типы оптимальности имеют разные «идейные основания»: основой оптимальности по Нэшу является устойчивость системы, обусловленная интересами и возможностями отдельных агентов, тогда как принцип оптимальности по Парето опирается на идею полезности, выгоды для системы в целом, понимаемой как выгода сразу для всех ее агентов.
Стандартные модели теории игр статичны в том смысле, что они сосредоточены на результатах переговоров, а не на процессе переговоров. В них также предполагается, что агент обладает полной информацией о своих собственных предпочтениях и функции полезности, а также о вероятностях, связанных с различными возможными результатами. Но на практике агент практически никогда не располагает точной информацией о предпочтениях других агентов. Принимая решение, он должен прогнозировать действия других агентов, выбор, которых, в свою очередь, зависит от его собственных действий. Это ведет к появлению эффекта «ограниченного прогнозирования», когда невозможно сделать точный прогноз или достоверно определить четкую стратегию индивидуального выбора.
Для того чтобы обойти этот эффект ограниченного прогнозирования, в традиционных моделях теории игр накладывают следующие ограничения: 1) предполагается, что количество агентов и их индивидуальные характеристики зафиксированы и известны всем агентам; 2) предполагается, что все агенты разумны и каждый агент, знает, что все остальные агенты разумны (аксиома общего знания); соответственно, набор альтернатив для каждого игрока зафиксирован и известен; 3) выдвигается допущение, что тип поведения каждого агента также зафиксирован и известен всем агентам.
Например, знаменитая игровая схема фон Неймана- Моргенштерна, (антагонистическая игра двух лиц или двух коалиций) основана на том факте, что в случае двух агентов-участников и игры с нулевой суммой эффекта ограниченного прогнозирования можно избежать следующим образом: каждый агент считает, что его оппонент будет всегда выбирать самый худший для своего визави вариант поведения.
Все эти предположения несколько ограничивают сферу применения традиционной теории игр и моделей основанных на ней для формализации взаимодействия партнеров в рамках сети виртуального предприятия.
Моделирование взаимодействия агентов в сети уделено много внимания в теории многоагентных систем (МАС), где исследователи придают особое значение построению протоколов взаимодействия, объясняющим компромиссы между агентами [85]. При этом структуру взаимодействия можно представить как пример последовательного принятия решений.
Основные характеристики модели последовательного принятия решений в таковы: 1) существует последовательность точек принятия решения агентами, которые зависят друг от друга; 2) у лица, принимающего решение, есть возможность, установив обратную связь по результату решения, обновить свои знания для того, чтобы на следующей стадии принимать решение с большей информацией.
В настоящее время механизм последовательного принятия решений является основой, на которой базируются различные модели ведения переговоров. Во-первых, большинство схем переговоров сводится к обмену предложениями и контрпредложениями. Структура последовательного принятия решений предлагает легко доступные конструкции для моделирования повторяющегося характера взаимодействия между агентами. Во-вторых, агенты, ведущие переговоры, действительно устанавливают обратную связь после того, как было сделано предложение или контрпредложение. Обратная связь заключается в ответе агента (или агентов), которому предназначалось предложение или контрпредложение. В-третьих, структура последовательного принятия решений поддерживает подход «открытого мира». При этом агенту не обязательно иметь полную информацию о своем окружении в начале переговоров. Приобретаемые в процессе переговоров знания обеспечивают обучение агента.
Наиболее распространенными специальными моделями взаимодействия агентов, используемых при моделировании и программно-аппаратной реализации многоагентных систем, являются [85]: модель контрактных (договорных) сетей Смита; модель социальных зависимостей. модель теории полезности с минимальными уступками; модель аукциона;
Модели контрактных (договорных) сетей
Модель контрактных (договорных) сетей, разработанная в начале 80-х гг. Р. Смитом [85], предназначена для обеспечения координации агентов в системах распределенного решения задач. Каждый узел сети - это агент, способный выполнять определенные задачи. Если в процессе решения задачи один агент (заказчик) оказывается не в состоянии найти решение самостоятельно, то он обращается к другим агентам - потенциальным исполнителям. Обычно он это делает не сам, а через агента-менеджера (брокера, администратора). Поскольку на запрос заказчика обычно откликаются несколько агентов, организуется конкурс на выбор наиболее подходящего подрядчика. При этом используется механизм торгов. Из числа потенциальных агентов-исполнителей выбирается реальный исполнитель - подрядчик. В результате между заказчиком и победившим в конкурсе агентом заключается договор. Ему предшествует итеративный процесс переговоров между агентом-менеджером и агентом-подрядчиком по вопросу определения итоговой цены контракта.
На рис. 1.5. представлена схема переговоров
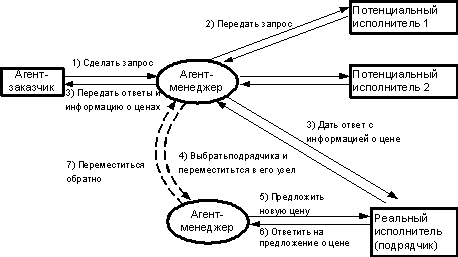
Рис. 1.5. Представление процесса координации в модели договорных сетей
Исходя из этой модели, процесс взаимодействия агентов можно описать набором [85]:
INT = (A, RR, r, P),
где А - множество агентов; RR - множество ролей агентов; р : А ® RR - функция распределения ролей; Р - общий протокол взаимодействий между агентами, Р = {COM, SRT, p}, СОМ - множество коммуникативных действий агентов; STR - множество стратегий взаимодействия; p - протоколы для отдельных ролей.
В данном случае RR = {заказчик, посредник, потенциальный исполнитель, подрядчик}, r(а0) = заказчик, r (а1) = посредник, r (а2) = подрядчик, r (а3) = ... = r (аn) = потенциальный исполнитель. Протокол взаимодействия представляет собой множество правил, управляющих взаимодействием. Для его определения помимо типов взаимодействующих агентов необходимо задать множество возможных состояний их взаимодействия (например, заказ выполнен, запрос принят, взаимодействие закончено), возможные действия агентов и стратегии взаимодействия. Простейшее множество действий может быть задано в виде СОМ = {начать, закончить, объявить, сообщить, предложить, принять, отвергнуть, оплатить}. Стратегия взаимодействия может определяться знанием предыдущего состояния партнера и информацией о текущем процессе взаимодействия.
Основное преимущество модели договорных сетей состоит в ее простоте и легкости программно-аппаратной реализации. К числу недостатков данной модели относятся отсутствие продуманного механизма выбора исполнителя и высокая загрузка коммуникационных каналов. Кроме того, модель договорных сетей не препятствует появлению таких агентов-посредников, которые выступают как спекулянты, покупая и перепродавая одну и ту же задачу несколько раз.
Известны различные усовершенствования модели Смита. Например, могут вводиться специальные промежуточные агенты-консультанты, роль которых состоит в оказании помощи координаторам при оповещении потенциальных исполнителей и обработке предложений. На сегодня самым удачным вариантом развития модели договорных сетей считается комбинированная модель Т. Сандхольма [85], где агентам-подрядчикам разрешено выполнять одновременно несколько задач. Для каждого подрядчика формируется пакет текущих задач, причем при добавлении к этому пакету новой задачи учитываются не только ее характеристики, но и уже принятые обязательства.
Модели социальных зависимостей
Суть теории социальных зависимостей заключается в том, что коллективная деятельность любых агентов всегда основывается на отношениях социальных зависимостей и общественной власти. При этом считается, что они являются составляющими компонентами когнитивных структур агентов.
В теории социальных зависимостей рассматриваются два основных типа зависимостей: 1) зависимость по отношению к действию и 2) зависимость по отношению к ресурсу. Обозначим через ACT(ai) множество всех действий, которые способен выполнять агент аi, а через RES(ai) - множество всех доступных ему ресурсов, Пусть pl(ai) - план действий агента аi для достижения его цели oi. Множество ACT (ai,pl) состоит из всех действий по выполнению плана pl(ai), а множество RES(ai,pl) - из всех ресурсов для выполнения плана pl(ai). На практике чаще всего набор индивидуальных ресурсов и репертуар индивидуальных действий агент ai, оказываются недостаточными для реализации плана. Обращение агент аi к другим агентам порождает его зависимость от них.
Понятие ресурсной зависимости вводится следующим образом. Пусть имеется некоторый ресурс res Î RES. Если res Ï RES(aj), но res Î RES(aj), то агент ai зависит от агента aj в плане ресурса res.
Аналогичным образом определяется понятие зависимости от действия. Пусть act Î ACT. Если act Ï АСТ(аi), но act Î ACT(aj), то агент агент аi зависит от агента aj в смысле действия act.
Отношение ресурсной зависимости является обоюдным тогда и только тогда, когда агент аi зависит от агента aj по отношению к ресурсу res(aj) и, напротив, агент aj зависит от агента аi, по отношению к ресурсу res(aj). Аналогично вводится обоюдная зависимость по отношению к действиям.
Анализ отношений зависимостей позволяет находить совместное решение задач. Например, если агенты аi и аj находятся в отношении обоюдной ресурсной зависимости и сознают это, то им обоим выгодно начать переговоры об обмене ресурсами. Кроме взаимного обмена ресурсами, возможны и другие кооперативные решения: составление совместного плана, купля-продажа ресурсов и т.д.
Теория социальных зависимостей имеет ряд недостатков:
1. Агенты не располагают стимулами для осуществления кооперации. Рассмотрим ситуацию, когда агент аi, односторонне зависит от агента ai в плане требуемого ресурса res(aj). После установления зависимости между обоими агентами, агент aj не располагает стимулами для передачи своего ресурса агенту аi.
2. В стандартной теории социальных зависимостей при определении отношения зависимости рассматриваются только один нуждающийся агент и только один поставщик ресурсов. Ситуации, в которых участвуют несколько агентов, нуждающихся в одном и том же ресурсе, и несколько поставщиков этого ресурса, не моделируются. Также не учитываются возможности коллективного применения ресурсов и одновременного оказания помощи одному агенту несколькими агентами.
3. В теории социальных зависимостей отсутствуют определения коллективной зависимости: зависимости одного агента от группы и зависимость группы агентов от одного агента.
Модели теории полезности с минимальными уступками
Среди протоколов ведения переговоров при моделирование многоагентных систем широкое распространение получил протокол монотонных минимальных уступок [85], который определяет процесс ведения переговоров между двумя агентами. Суть его заключается в следующем. Агенты делают предложения по очереди, начиная с самых выгодных для себя условий. Затем в процессе переговоров агенты монотонно отступают от своих первоначальных требований, т.е. функция полезности каждого агента монотонно убывает на последовательности его предложений. Доказывается, что в результате переговоров агенты выбирают то соглашение, которое максимизирует произведение их функций полезности. Множество возможных соглашений в протоколе монотонных минимальных уступок состоит из всех индивидуально рациональных соглашений, эффективных по Парето.
Множество схем организации переговоров можно представить себе как варианты подобной двусторонней модели, согласно которой переговорный процесс рассматривается как последовательность контрпредложений, выдвигаемых двумя взаимодействующими агентами.
Модели аукциона
Аукцион является мощным рыночным механизмом самоорганизации и коллективного поведения. С его помощью, как и в моделях, основанных на теории игр, можно реализовать такую схему торгов, которая обеспечит требуемые свойства системы [85]. Использование механизма аукциона в переговорах агентов обеспечивает возможность явной передачи «полезности» от одного агента к другому.
На аукционе некоторые ресурсы, необходимые для достижения цели несколькими агентами, выставляются на продажу. Ресурсы эти ограничены, поэтому агенты соперничают между собой в процессе торгов. Возможности покупки ресурсов агентами также ограничены, а целесообразность покупки оценивается функцией полезности ресурса, которая, как правило, вычисляется в виде разности между доходом от использования ресурса и затратами на его покупку.
На аукционе один агент играет роль аукционера. Только он заинтересован в повышении цены на ресурс. Все остальные агенты заинтересованы в снижении цен.
Аукционы могут проводиться по различным схемам, причем результаты торгов существенно зависят от этого. Так аукционы бывают открытыми и закрытыми. На открытых аукционах цены объявляются публично, и каждый участник знает о ценах, предлагаемых другими участниками. На аукционах закрытого типа цены известны только аукционеру.
Аукционы открытого типа, в свою очередь, делятся на:
• «английские», когда цена повышается, начиная с некоторой стартовой, и побеждает тот агент, кто предложил наибольшую цену;
• «голландские», когда торги начинаются с самой высокой цены, за которую агент-аукционер хотел бы продать ресурс, и эта цена им постепенно снижается, пока какой-либо агент не согласится купить ресурс за предлагаемую цену.
На аукционах со скрываемыми ценами принято различать так называемые аукционы первой и второй цены. В аукционах первой цены побеждает тот, кто предложит наибольшую цену (известную только аукционеру; именно эту цену победитель аукциона и платит). В аукционах второй цены победитель определяется таким же образом, однако, он выплачивает не ту сумму, которую предложил, а вторую по порядку. Также могут существовать аукционы, в которых агенты образуют коалиции с последующей заранее согласованной политикой использования купленного ресурса.
Описанные специальные модели взаимодействия агентов, используемых при моделировании и программной реализации многоагентных систем, могут быть использованы при программной реализации системы организации и управления виртуальным предприятием, в частности для задач подбора партнеров для выполнения заказов.
В целом, исследование существующих моделей формирования и управления организационными системами показало, что вопросам формирования состава участников и организации эффективной сетевой структуры уделено мало внимания, и применение существующих моделей на практике затруднительно в силу использования либо «абстрактных» функций, либо ориентация только на финансовые аспекты деятельности партнеров.
В то же время, в теории активных систем и близких к ней направлениях теории управления социально-экономическими системами разработано множество механизмов управления, ориентированных на те или иные прикладные задачи и ситуации и характеризуемых частным видом целевых функций, специфичными информированностью и порядком функционирования. Поэтому значительный интерес представляет более глубокое исследование и разработка моделей и механизмов (инструментов) формирования состава и структуры участников долгосрочного виртуального предприятия как для функционирования всего предприятия, так и для выполнения отдельных заказов и проектов.
| Предыдущая |