Помогите решить задачи по дисциплине "Методы оптимальных решений" с решением.

День добрый.
Очень нужно решение по данным задачам.
Спасибо!!!!

Понимаете ли: Эксель изначально заточен под алгоритм "Симплексный метод", его коронный номер?
На Эксель можно каждую из Ваших задач решить за 2-3 минуты. Например, смотрите картинку и вложение по первому заданию, ниже.


Мне непонятно: по каким именно образцам надо решать Ваши задачи? Где методические указания с примерами решений, должны быть у Вас. Прикрепите их как вложение.

Рисовать мне не на чем, под рукой только — Pain. Он примитивен.

Вторая задача:
20x1 + 30x2 —> max
x1 + 2x2 =< 10;
x1 + x2 =< 6;
x2 =< 3;
x1 => 0; x2 = > 0.
Ответ: x1 = 3; x2 = 3; max = 150.

Четвёртая (третья по реальным) задача

Третью задачу нужно было решить графическим методом.
На все эти задачи в сети до кучи онлайн-калькуляторов с пошаговым решением есть. Лень поискать было?
[...]
[...]
[...]

Это, выше, ерунда... много воды!

Лучше скачать Методичку, всего 65 страниц. Очень много хороших графических примеров с пояснениями.

На страницах 11-14
1.4. Примеры графического метода решения задач линейного программирования
Задача 1.
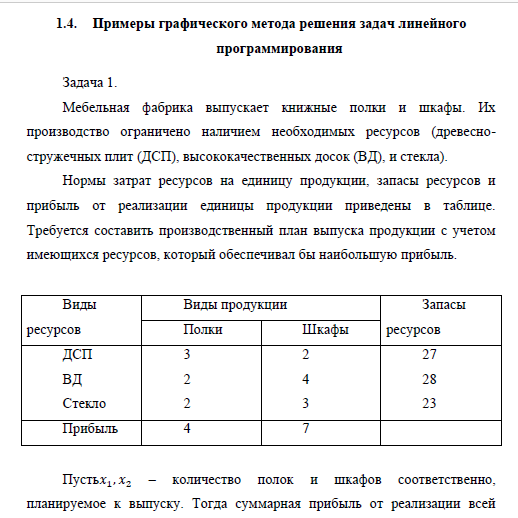
Мебельная фабрика выпускает книжные полки и шкафы. Их производство ограничено наличием необходимых ресурсов (древесно-стружечных плит (ДСП), высококачественных досок (ВД), и стекла).
Нормы затрат ресурсов на единицу продукции, запасы ресурсов и прибыль от реализации единицы продукции приведены в таблице. Требуется составить производственный план выпуска продукции с учетом имеющихся ресурсов, который обеспечивал бы наибольшую прибыль.

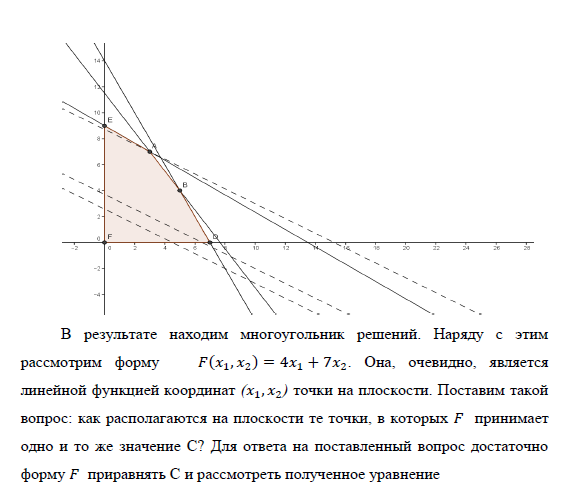
Пусть x1, x2 – количество полок и шкафов соответственно, планируемое к выпуску. Тогда суммарная прибыль от реализации всей плановой продукции (целевая функция) составит: F(x1,x2) = 4x1 + 7x2 —> max . При этом общий расход ДСП равен: 2x1 + 3x2 , и он не должен превышать имеющегося запаса 27. Это приводит к ограничению 2x1 + 3x2 ≤ 27. Аналогично учитываются ограничения по ВД и стеклу: 2x1 + 4x2 ≤ 28 , 2x1 + 3x2 ≤ 23. Так как объемы выпускаемых изделий не могут быть отрицательны, то x1 ≥ 0, x2 ≥ 0.

Итак, математическая модель задачи имеет вид:
F(x1,x2) = 4x1 + 7x2 —> max
Система:
2x1 + 3x2 ≤ 27
2x1 + 4x2 ≤ 28
2x1 + 3x2 ≤ 23
x1 ≥ 0, x2 ≥ 0

Надо просто решить систему уравнений:
2x1 + 3x2 =27
2x1 + 4x2 = 28
2x1 + 3x2 = 23
x1 = 0, x2 = 0

Мне непонятно: по каким именно образцам надо решать Ваши задачи? Где методические указания с примерами решений, должны быть у Вас. Прикрепите их как вложение.

Вот: [...]

Это у Вас от Зенкевича, очень мутно и бестолково.
Надо запросом
Google: Создание банка тестовых заданий по теме «Графический метод решения задач линейного программирования»

У меня самый первый по странице:
[PDF] Графический метод решения задач линейного программирования
kpfu.ru/portal/docs/F1802830430/Nurieva.pdf‎
Создание банка тестовых заданий по теме «Графический метод решения задач ... Примеры графического метода решения задач линейного.

Или так по ссылке, скачать 1954 Кб: [...]

Там выше маленькая описка, смотрите предыдущий мой пост. Правильно будет:
Итак, математическая модель задачи имеет вид:
F(x1,x2) = 4x1 + 7x2 —> max
Система:
3x1 + 2x2 ≤ 27
2x1 + 4x2 ≤ 28
2x1 + 3x2 ≤ 23
x1 ≥ 0, x2 ≥ 0

Надо просто решить систему уравнений:
3x1 + 2x2 =27
2x1 + 4x2 = 28
2x1 + 3x2 = 23
x1 = 0, x2 = 0

Например, находите две точки и проводите прямую:
3x1 + 2x2 =27; x1 = 0 и x2 = 13.5; x1 = 9 и x2 = 0;
2x1 + 4x2 = 28; x1 = 0 и x2 = 7; x1 = 14 и x2 = 0;
2x1 + 3x2 = 23; x1 = 0 и x2 = 7.67; x1 = 11.5 и x2 = 0;

Проведёте три прямые через точки (x2 = 13.5; x1 = 9), (x2 = 7; x1 = 14) и (x2 = 7.67; x1 = 11.5). Смотрите график выше.

Затем в 4-м квадранте указываете точки (x2 = 7; x1 = -4). Проводите ещё одну прямую через начало координат и эти точки.

Далее в 1-м квадранте указываете точки (x2 = 4; x1 = 7). Проводите через них и начало координат опять прямую. Она будет являться перпендикуляром к предыдущей в 4-м квадранте.

Остальное позже поясню.