Модели распределения заказов - Катаев А.В. Виртуальные бизнес-организации

А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.

3.1. Модели распределения заказов

Одним из основных этапов эффективного управления виртуальным предприятием является оптимальное и оперативное распределение заказов среди партнеров (агентов) виртуального предприятия.

В параграфе 1.4. приводятся модели размещения центром заказа среди n партнеров, когда партнеры (агенты) взаимодействуют между собой и с центром с целью получения заказа на производство. Цель центра - размещение заказа с минимальными затратами 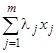, цель каждого из агентов - максимизация прибыли, определяемой как разность между вознаграждением, выплачиваемым центром, и собственными затратами. При этом известны - удельные переменные издержки i-го предприятия по производству -го вида продукции, - постоянные издержки i-го предприятия, - объем выпуска j-го продукта на i-м предприятии, - суммарное количество продукции j-го вида, требуемое в заказе, - заказ выпуска j-го продукта i-му предприятию, - цена, установленная заказчиком (центром) на единицу продукции j-го вида, .

Как отмечено выше, во-первых, подобные модели применимы в том случае, когда заказ однороден, может быть разбит на части и размещен на разных предприятиях, что характерно для производственных предприятий, когда выпускается одинаковая продукция. Причем, центру необходимо знать либо иметь возможность оценить затраты партнеров на выполнения заказа, что является практически невозможно в условиях независимых агентов. Во-вторых, основной целью оптимизации выступает максимизация прибылb или минимизация затрат центра и участников, а не степень удовлетворения потребностей конечного заказчика, что является немаловажным в условиях жесткой конкуренции и ориентации на конечного потребителя.

Таким образом, при исследовании и разработке моделей необходимо учесть следующие условия:

1. Критерии и процедуры оценки и отбора партнеров (исполнителей заказа) должны быть четко установлены, «прозрачны» и понятны всем участникам сети, которые конкурируют за получение заказа.

2. Целесообразно минимальное участие и влияние администратора (центра, руководителя, координатора) в процессе распределения заказов, т.е. процедуры распределения заказов должны осуществляться максимально автоматически, устраняя предпочтения и субъективное мнение администратора.

В ходе исследования выделены три вида задач распределения заказов в рамках виртуального предприятия:

1) задачи оперативного выбора агента, который наилучшим образом может выполнить поступивший заказ (задачи выбора агента для выполнения заказа);

2) задачи оптимального распределения совокупности партнеров (агентов) на выполнения совокупности заказов за определенный период времени, когда один заказ полностью выполняется только одним агентом (задачи оптимального распределения совокупности заказов) и заказы не связаны и независимы.

3) задачи оптимального распределения заказа по агентам, когда один заказ требует участия нескольких агентов, т.е. задачи распределения заказа по совокупности партнеров (см. п. 3.2.).

Общим в этих задачах является оценка и выбор исполнителя для выполнения определенного заказа (задачи), наиболее отвечающего требованиям заказа.

В этой связи выделены следующие группы характеристик заказа, которые могут выступать и как критерии оптимальности, и как ограничения:

1) стоимостные характеристики заказа;

2) временные характеристики выполнения заказа;

3) характеристики качества выполнения заказа;

4) количественные характеристики заказа.

В общем случае при выборе и распределение партнеров по заказам необходимо с одной стороны минимизировать стоимостные характеристики выполнения заказа и время выполнение заказа, а с другой – с максимизировать качество и количественных характеристик выполнения заказа.

Учитывая, что полной информацией по независимым и автономным агентам и их возможностям нет, необходимо производить оценку и отбор по той информации, которую они предоставляют сами, и по внешним результатам и оценкам их деятельности как в целом, так и в рамках виртуального предприятия.

По этим и другим показателям могут быть введены ограничения (фильтры) при первоначальном отборе потенциальных исполнителей заказа из всей совокупности агентов и при оптимизации распределения заказов. Эти критерии могут быть решающими при возникновении «конфликтных» случаев, когда по всем параметрам один заказ одинаково могут выполнить несколько партнеров.

Показатель уровня компетенции агента может служить критерием максимизации качества выполнения заказа, т.е. для увеличения качества выполнения заказа необходимо выбирать агентов с максимальным уровнем компетенции по требуемой сфере деятельности или задаче.

Далее рассмотрим задачи распределения заказов и возможные методы решения.

Задача распределения совокупности заказов по совокупности агентов может быть сформулирована как задача о назначениях. Классическая постановка однокритериальной задачи о назначениях в исследовании операций [1, 20 и др.] состоит в нахождение пар «Исполнитель – Работа», которые обеспечивают минимум суммарных затрат на выполнение всех работ, причем каждый исполнитель выполняет только одну работу и для одной работы требуется только один исполнитель, т.е. исполнители не делимы между работами, а работы не делимы между исполнителями. Таким образом, задача о назначениях является частным случаем транспортной задачи. Задачи о назначениях имеют место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины и т.п.

В таблице 3.1. приведена матрица задачи о назначениях по типу транспортной задачи.

Таблица 3.1

Общий вид матрицы задачи о назначениях

Исполнители,	Работы,				Количество исполнителей
Исполнители,			…		Количество исполнителей
			…		1
			…		1
…	…	…	…	…	…
			…		1
Количество работ	1	1	…	1

Исходные параметры модели задачи о назначениях:

1. n – количество исполнителей, m – количество работ;

2. – единичное количество ресурса (), например: один работник, одно транспортное средство, одна научная тема и т.д.

3. – единичное количество работы (), например: одна должность, один маршрут, одна лаборатория.

4. – стоимость выполнения работы с помощью ресурса . Например, с_ij может быть компетентностью i-го работника при работе на j-й должности; временем, за которое i-е транспортное средство перевезет груз по j-му маршруту; степенью квалификации i-й лаборатории при работе над j-й научной темой.

Искомые параметры

1. – факт назначения или «неназначения» исполнителя на работу :

2. – общая (суммарная) характеристика качества распределения исполнителей по работам.

Общий вид модели задачи о назначениях

. (3.1)

Пример задачи:

Необходимо распределить заказы по партнерам, чтобы суммарная стоимость (цена, внутренняя стоимость) выполнения совокупности заказов (задач) была минимальна. Решение данной задачи предполагает, что:

1) сроки, объемы и качество выполнения фиксированы для каждого заказа (устанавливаются заказчиком либо менеджером как необходимое требование);

2) возможность выполнения и стоимость (внутренняя стоимость) выполнения определенного заказа сообщается каждым партнером после предоставления требований и условий заказа (можно через аукционы) либо известна заранее по каждому партнеру для типовых заказов (например, тарифы для перевозок груза, цена на размещения рекламных сообщений, расценки по аренде помещений и т.п.);

Следует заметить, что для решения данной задачи с помощью модели (3.1) n должно равняться m. В случае несовпадения количества исполнителей и работ, необходимо ввести либо фиктивные работы, либо фиктивных исполнителей с присвоением заведомо больших значений (запрет) – больше максимального не фиктивных значений.

Задача о назначениях в таком виде может быть решена с помощью «венгерского метода», «симплекс-метода» и др. В некоторых случаях, например, когда – это компетентность, опыт работы, или квалификация работников, условие задачи может требовать максимизации ЦФ, в отличие от (3.6). В этом случае ЦФ заменяется на и решают задачу с ЦФ , что равносильно решению задачи с ЦФ .

Задачу о назначениях можно сформулировать также в терминах теории графов. В этом случае G (X, Y, E, C) представляет собой взвешенный двудольный граф, где: доля X={x₁, …, x_i, x_m} – множество объектов (вершин графа), представляющие исполнителей; доля Y = {y₁, …, y_j, y_m} - множество объектов (вершин графа), представляющие работы (задачи); E – множество всех возможных пар (x_i, y_j) размерностью m*n; C – матрица весов двудольного графа G, c_ij – стоимость образования пары (x_i, y_j).

Задача о назначении в теории графов решается на основе алгоритма нахождения кратчайшей сети Крускала [97]. Применительно к двудольному графу алгоритм решения задачи для случая m<=n (число исполнителей меньше количества работ) имеет следующий вид:

1. В каждой строке матрицы С находится элемент , i = 1, …, m. Т.е. минимальный по величине элемент.

2. Если все элементы принадлежат разным столбцам, то решением задачи является пары (x_i, y_i), соответствующие элементам по каждой строке. В противном случае выполняется п. 3.

3. Для j-го столбца матрицы j = 1, …n, выполняется анализ:

3.1. Если элемент и принадлежат одному (j-му) столбцу матрицы, в i-й и k-й строках находятся следующие по величине элементы и .

3.2. Вычисляются разности и .

3.3. Если , то вместо принимается , иначе вместо принимается .

Для распределения заказов в классическом виде модель задачи о назначениях мало применима в связи с ограничением по количеству заказов, которое может взять один исполнитель (в классическом виде один исполнитель может взять только один заказ). В реальных же условиях функционирования виртуального предприятия один партнер в определенный период времени может выполнять множество заказов с ограничением по количеству типовых заказов. Например, при выполнении дизайна сайта, разработки рекламных баннеров, проведении кабинетных исследований рынков, аудиту и т.п. партнеры, специализирующиеся на этом, могут оценить собственные возможности по количеству типовых заказов (проектов) в определенный период времени.

Представляя и решая задачу в виде задачи линейного программирования можно устранить это требование и получить модель для распределения типовых заказов:

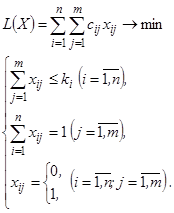, (3.2)

где - количество возможных заказов.

В постановке (3.2) не требуется совпадение количества исполнителей и работ в модели, однако задача должна решаться целочисленными методами, т.е. и (0 или 1). Могут быть добавлены ограничения на невозможность, отказ или запрет выполнения работ i-ым партнером j-ого заказа ; либо обязательное (приоритетное) выполнение i-ым партнером j-го заказа (например, предпочтение заказчика) .

Запреты и предпочтения могут быть проставлены по примеру транспортной задачи путем присвоения значений заведомо больших значений (больше максимального ) – запрет или заведомо меньших значений – предпочтение.

Когда заказы не типовые, но используются типовые ресурсы (количество сотрудников, фонд времени, площади и т.п.) для их выполнения, модель можно записать в виде 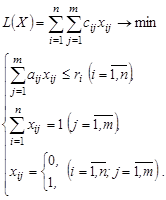(3.3):

, (3.3)

где - количество (объем) требуемых ресурсов для выполнения заказа; - возможное количество (объем) ресурсов, которое может выделить партнер для выполнения заказов.

Рассмотренные модели и задачи применимы в случае одного критерия оптимальности. На практике же приходится принимать решения, учитывая несколько критериев.

В работе [59] задача о назначении получила развитие на случай многих критериев. В этой постановке каждый исполнитель , , характеризуется некоторой совокупностью критериев . С другой стороны, каждая работа , , характеризуется перечнем требований к исполнителю . По сути, эта задача отличается от классической задачи о назначении персонализацией как исполнителей, так и работ. Ее можно решать как со стороны исполнителей – подобрать каждому из них работу, так и каждой работе подобрать наиболее соответствующего исполнителя.

Если пространство критериев и предъявляемых к ним требований совпадают, под решением сформулированной задачи понимается совокупность пар (y_j, x_i), обладающих максимальной степенью соответствия между требованиями к исполнителю и значениями характеризующих его критериев . В [59] описанная задача названа «многокритериальной задачей о назначениях» (МЗН). В [64] она называется «задачей многокритериального соответствия» (ЗМС) между возможным и желаемым.

Одна из содержательных постановок такой задачи была дана в [89]. В ней рукописи, поступившие в издательство, распределялись между сотрудниками. Каждая рукопись характеризовалась тематикой, важностью, срочностью исполнения работы. Каждый работник, в свою очередь, характеризовался специализацией (предпочитаемой тематикой), качеством работы, производительностью труда.

В идеальном случае для каждой пары (x_i_,y_j), , , имеет место полное соответствие векторов и , т.е. их элементы попарно раны. Это означает, что для декартова произведения можно подобрать функциональное соответствие между всеми элементами их множеств Y и X. Однако на практике такая ситуация встречается не часто. Следовательно, необходимо искать максимальное значение количество наилучших возможных назначений. Под наилучшим понимается такое назначение (x_i_,y_j) для которого имеет место максимальное совпадение векторов.

Для покомпонетного сопоставления векторов c_i и r_i достаточно номинальной шкалы. Она применима для сопоставления не только числовых, но и вербальных значений переменных, которые применяются при экспертном оценивание работ и исполнителей. В [59] для сопоставления векторов c_i и r_i используется порядковая шкала. Ее применение преследует цель ранжирования всех претендентов на назначение относительно степени соответствия векторов c_i и r_i. Ранжирование выполняется на основе суммирования несовпадающих компонент векторов для каждой пары (x_i_,y_j), , и упорядочения претендентов в направлении увеличения сумм.

К недостаткам модели и метода решения, предложенного в [59], можно отнести следующее:

1. Для упорядочения претендентов используется грубая порядковая шкала. На практике же критерии могут иметь численные значения и измеряться в интервальной шкале. В этом случае интересует не только число совпадений значений, но и величина несовпадения.

2. Предполагается однородность оценок несовпадения. Как правило, критерии разнородны и нуждаются в нормализации.

3. Предполагается равная значимость критериев в векторах x_i и y_j. На практике критерии, характеризующие возможности исполнителя и требования со стороны работы, как правило, неравноценны, т.е. необходимо учитывать значимость (важность) этих критериев.

4. Ориентация только на совпадение предложений с требованиями с заданием точечных значений. В случае, если есть исполнитель, который полностью соответствует требованиям, и исполнитель с характеристиками выше требований, то предпочтение будет отдано первому, а не второму.

Перечисленные недостатки сужают область применения данной модели и метода решения. Они могут быть использованы только в частных случаях задачи распределения заказов в рамках виртуального предприятия.

Таким образом, за основу примем однокритериальные модели распределения заказов. Как было ранее показано, часть задач распределения заказов (частные случаи) может быть сформулирована в виде моделей (3.1), (3.2) и (3.3). Причем модель вида (3.2) при снятии ограничения для количества заказов легко решается путем нахождения минимальных по каждому заказу, без применения методов линейного программирования, т.е. линейная модель вырождается в простой выбор партнера, обеспечивающего наилучшее выполнения проекта.

Трудность принятия решений при использовании данных моделей возникает при количестве минимальных значений для одного заказа больше одного, т.е. когда на выполнение заказа претендуют несколько партнеров, имеющих одинаковые показатели. В данном случае, рекомендуется заранее сформировать решающие критерии – показатели по которым будет отдаваться предпочтение одному из партнеров при прочих равных условиях. Например, решающими критериям могут быть срок участия в сети партнера, время ответа на заявку и др.

Далее необходимо разработка общего подхода (алгоритма) распределения заказов в рамках виртуального предприятия на основе многокритериального выбора с использованием рассмотренных методов и моделей.

Для решения многокритериальных задач (задач многокритериального выбора) известен ряд методов, которые можно разделить на четыре группы:

1. Сведение многих критериев к одному путем введения весовых коэффициентов важности для каждого критерия и нормализации векторного критерия.

2. Минимизация максимальных отклонений от наилучших значений по всем критериям;

3. Оптимизация одного критерия, а остальные критерии выступают в роли дополнительных ограничений;

4. Ранжирование множества критериев и последовательная оптимизация по каждому из них.

Далее построим модели распределения заказов (3.5) и (3.6) с учетом трех критериев – стоимость (матрица С), компетентность исполнителя (матрица Q), время выполнения заказа (матрица T).

Учитывая, что значения критериев имеют различные единицы измерения, приведем их к безразмерному виду и произведем свертку с учетом важности каждого критерия. В итоге получим матрицу интегральных коэффициентов (суперкритериев) SK, элементы которой можно получить по следующей формуле:

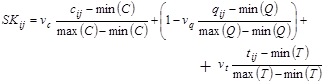, (3.4)

где SK – матрица интегральных коэффициентов; , , - коэффициенты важности соответствующих критериев, причем .

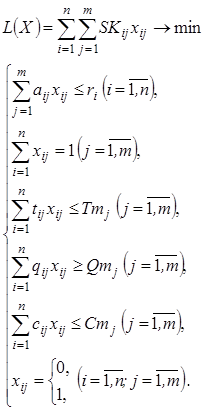(3.5)

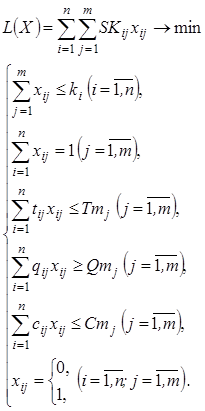(3.6)

где - количество возможных заказов; - количество (объем) требуемых ресурсов для выполнения заказа; - возможное количество (объем) ресурсов, которое может выделить партнер для выполнения всех заказов; - максимальное время, за которое необходимо выполнить j-й заказ; - минимальная компетенция партнера, которая необходима для выполнения j-го заказа; - максимальная стоимость выполнения j-го заказа.

В постановках (3.5) и (3.6) не требуется совпадение количества исполнителей и работ в модели, также учтены возможные ограничения по стоимости заказа, времени и качеству его выполнения.

Модели (3.5) и (3.6) должны решаться целочисленными методами, т.е. (0 или 1). Также могут быть добавлены ограничения на невозможность (отказа, запрет) или предпочтение выполнения работ i-м партнером j-го заказа.

Построены модели распределения независимых заказов при условии, что один заказ полностью может быть выполнен одним партнером.

Далее рассмотрим задачи, когда один заказ не может быть выполнен одним партнером и необходимо оптимальным образом подобрать исполнителей (партнеров) на выполнение проекта.

Оглавление

Глава 3. Модели распределения партнеров и заказов в долгосрочных виртуальных предприятиях

3.1. Модели распределения заказов