А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.
| Предыдущая |
Глава 3. Модели распределения партнеров и заказов в долгосрочных виртуальных предприятиях
3.2. Модели формирования сетей партнеров для реализации проектов
Одной из задач распределения заказов в рамках виртуального предприятия является задача оптимального распределения, когда один заказ не может быть выполнен при заданных параметрах одним партнером.
В ходе исследования, выделены четыре подхода к принятию решений по распределению заказов в данном случае:
1. Разбивка заказа на независимые части (подзаказы) и распределение их по партнерам, используя модели предложенные в п. 3.1. и п. 2.4.
2. Предварительная разбивка заказа на отдельные задачи (работы) и подбор партнеров под эти задачи. Данный подход применим в случае, когда администратор имеет информацию и возможность спроектировать выполнения заказа по этапам, работам, срокам, требуемым ресурсам и т.п.
3. Формирование группы партнеров, которой заказ перейдет полностью, на основе выделения ключевых компетенций, требуемых для выполнения заказа. Этот подход эффективен в том случае, если администратор может выделить необходимые ключевые компетенции и общие требования, но не может спроектировать ход выполнения заказа по отдельным этапам, работам и т.п.
4. Определение партнера, который может наилучшим образом выполнить или организовать выполнение заказа, а затем вместе с этим партнером находятся пути улучшения параметров (сроков, качества, стоимости и т.п.) выполнения заказа за счет передачи отдельных задач (работ) другим партнерам. Данных подход можно применять в том случае, когда нет возможности применить предыдущие.
В случае, когда нет возможности разбить заказ на невзаимосвязанные и независимые работы, предлагается воспользоваться методами управления проектами и сетевого планирования и управления (СПУ)[1]. СПУ - один из подходов к управлению сложными динамическими системами с целью обеспечения определенных оптимальных показателей, таких как установление продолжительности выполнения работ коллективами исполнителей, равномерное распределение ресурсов по видам работ, сокращение срока окончания всех работ при минимальном увеличении затрат и др.
Сетевое планирование и управление включает три основных этапа: структурное планирование, календарное планирование и оперативное управление.
Этап структурного планирования начинается с разбиения проекта на четко определенные работы. Затем определяются оценки продолжительности операций (задач, работ) и строится сетевой график (сетевая модель, стрелочная диаграмма), каждая дуга которого отображает работу. Вся сетевая модель в целом является графическим представлением взаимосвязей работ проекта.
Сетевой график отображает взаимосвязи между работами и порядок их выполнения. Событие определяется как момент времени, когда завершаются одни работы и начинаются другие. Начальная и конечная точки любой работы описываются, таким образом, парой событий, которые называют обычно начальным и конечным событием. Каждая операция в сети представляется только одной дугой. Ни одна пара событий не должна определяться одинаковыми начальными и конечными событиями.
При построении сетевого графика в СПУ оцениваются продолжительность каждой работы и требуемые
ресурсы. Оценка продолжительности работы, как правило, определяется либо
однозначно по нормативным данным, либо по возможной продолжительности работы в
определенном диапазоне 
, где 
- продолжительность выполнения
работы при благоприятных условиях и обстоятельствах, дни (недели); 
- то же, при неблагоприятных
условиях и обстоятельствах, дни (недели). По этим исходным данным
рассчитывается ожидаемая продолжительность 
.
Предположим, что администратор знает только взаимосвязь работ и требования ко всему проекту в целом. В этом случае ему необходимо подобрать партнеров на каждую работу, которые наилучшим образом могут выполнить проект.
Далее, рассмотрим построение моделей распределения заказов на примере сетевого графика выполнения условного проекта (рис. 3.1.).
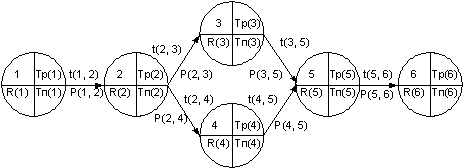
Рис. 3.1. Пример сетевого графика
где:
- ранний срок
наступления события s. Это время, которое необходимо для выполнения всех
работ, предшествующих данному событию s. Оно равно наибольшей из
продолжительности путей, предшествующих данному событию; 
- поздний срок
наступления события s. Это такое время наступления события s,
превышение которого вызовет аналогичную задержку наступления завершающего
события сети; 
- резерв времени наступления события s. Это такой
промежуток времени, на который может быть отсрочено наступление события s без
нарушения сроков завершения проекта в целом. 
; 
- работа (k, g),
где k - номер начального
события работы, а g – номер конечного; 
- время выполнения работы .
К наиболее важным временным параметрам работ
относятся: 
- ранний срок
начала работы; 
- поздний срок начала работы; 
- ранний срок окончания работы; 
- поздний срок окончания работы; 
- полный резерв работы показывает максимальное время, на которое
может быть увеличена продолжительность работы 
или
отсрочено ее начало, чтобы продолжительность проходящего через нее
максимального пути не превысила продолжительности критического пути; 
- свободный
резерв работы показывает максимальное время, на которое можно увеличить
продолжительность работы или отсрочить ее начало,
не меняя ранних сроков начала последующих работ. Использование свободного
резерва одной из работ не меняет величины свободных резервов остальных работ
сети.
Временные параметры работ сети можно определить на основе ранних и поздних сроков событий и длительностей этих работ:
1) 
;
2) 
или
;
3) 
;
4) 
или 
;
5) 
;
6) 
.
Зная временные параметры событий и резервы времени у работ, можно найти длительность работы:
(3.7)
Воспользовавшись этой формулой можно записать систему уравнений, описывающих топологию сети, приведенной на рис. 3.1:
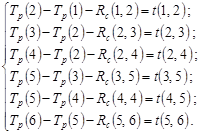
(3.8)
Зная значения длительностей работ
и принимая время
начального события равное нулю, можно найти остальные неизвестные, записав и
решив следующую линейную модель:
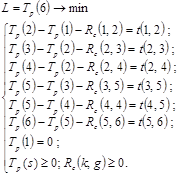(3.9)
Для оптимизации по трем критериям (цена, время и компетенция) нормализуем векторные критерии, введем коэффициенты важности критериев и произведем свертку к одному интегральному показателю:
, (3.14)
где SK – матрица интегральных показателей; 
, 
,
- коэффициенты важности соответствующих
критериев, причем 
;
Тогда можно построить следующую модель:
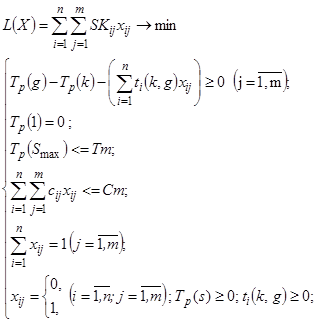(3.15)
где: 
- ранний срок наступления события s, .т.е. время, которое необходимо для
выполнения всех работ, предшествующих данному событию s;
и 
- ранние сроки наступления начального и
конченого события для работы ; 
- время выполнения работы i-ым партнером; 
и 
- максимальные длительность и стоимость выполнения всего заказа
соответственно; 
- срок наступления конечного для проекта события (срок
окончания проекта).
Модель (3.15) не учитывает тот факт, что определенные
партнеры могут начать и закончить работы только в определенные периоды времени.
Для учета этого ограничения в модели необходимы данные от каждого партнера
возможного начала работы 
и окончания 
, т.е. период времени, когда партнеры
свободны для выполнения работы.
Зная для каждого партнера по
каждой работе, можно записать ограничение следующего вида:
. (3.16)
Возможное окончание работы можно записать ограничением:
(3.17)
В неравенстве (3.17) не учтены возможные свободные
резервы времени у работ, получаемые при решении модели и конечном расчете
сетевой модели. Т.е. при использовании этого ограничения может быть подобран
партнер, который должен будет начать работу точно в и выполнить
за время , несмотря на то, что 
. Для устранения этого недостатка можно
ввести в модель в качестве неизвестных свободные резервы работ , убранные ранее.
Тогда ограничение запишется в виде:
, (3.18)
либо
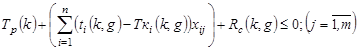. (3.19)
Тогда модель с ограничениями по возможным начальным и конечным срокам выполнения каждой работы партнерами запишется в виде (3.20).
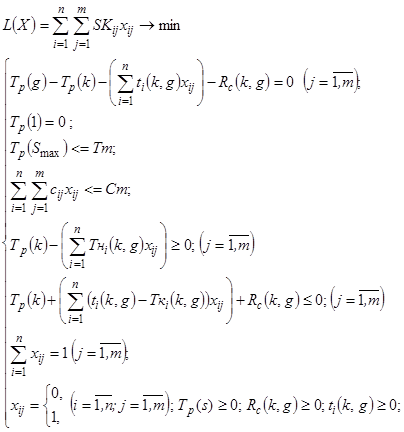(3.20)
Разработанная модель (3.20) позволяет оптимальным образом подобрать и распределить партнеров на выполнение работ проекта, учитывая:
- последовательность и взаимосвязь работ;
- возможные сроки начала и окончания планируемых работ (периоды времени, когда партнер может выполнить работу с заявляемыми параметрами);
- параметры выполнения отдельных работ и проекта в целом (время, цена, качество);
- невозможность выполнения работ тем или иным партнером.
[1] Моудер Дж., Филлипс С. Метод сетевого планирования и организации работ (Перт). - М-Л,: Энергия, 1966. Таха X. Введение в исследование операций. - М.: Мир, 1985
| Предыдущая |