А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.
| Предыдущая |
Глава 3. Модели распределения партнеров и заказов в долгосрочных виртуальных предприятиях
3.3. Модели распределения затрат при финансировании внутренних проектов
При функционировании долгосрочного виртуального предприятия возникают задачи связанные с разработкой проектов (создание новых технологий, исследовательские проекты, проектирование и наполнение баз данных и т.п.), которые необходимы для функционирования всего предприятия и могут использоваться всеми партнерами сети.
Такие проекты, как правило, финансируются не одним из партнеров или центром. Центр или инициаторы проекта стараются привлечь средства заинтересованных партнеров для реализации проекта. Задача финансирования в этом случае, очевидно, относится к классу задач распределения затрат [12].
Последний вывод следует из того, что каждый из исполнителей проекта заинтересован в производстве нового продукта, новой технологии, информации и т.п., т.е. успешной реализации проекта. Пользоваться этим продуктом будет каждый из участников проекта. Но для его производства необходимо создать бюджет проекта, что и приводит к задаче распределения затрат между участниками.
Если центру известен эффект каждого из исполнителей от использования продукта (от проекта в целом), то, очевидно, можно распределить затраты равными долями, пропорционально потребности в проекте и т.п. Однако на практике потребности партнеров известны только им самим и объявляются ими по принципу меньше затрат больше эффекта, преследуя цель реализации проекта за счет других исполнителей. Таким образом, возникает проблема манипулируемости, когда каждый из партнеров в общем случае может исказить информацию, манипулируя данными [57].
Рассмотрим сеть из двух партнеров, не считая центра. Обозначим доходы партнеров от реализации проекта как qi i=1,2, общие затраты на проект - С, затраты каждого из партнеров – С1 и С2, причем C1+C2=C.
Пусть С=1. Принцип равного распределения заключается в равенстве C1=C2=C/2. Если значения целевых функций парнеров fi=qi-Сi,- неотрицательны, т. е. q1>C/2 и q2>C/2, то такое распределение будет допустимым и немани-пулируемым. Однако, если априори известно, что q1≠q2, то справедливым было бы и С1≠С2, т.е. затраты каждого из исполнителей неодинаковы.
Принцип пропорционального распределения заключается в том, что затраты распределяются пропорционально эффекту от проекта для каждого из участников сети:
(3.21)
где S = s1 + s2, здесь si - сообщаемая центру оценка дохода i-го исполнителя.
Из (3.21) следует, что должно выполняться
(3.22)
поскольку иначе реализация проекта невыгодна в силу превышения затрат над суммарным доходом.
Для не отрицательности целевых функций ft предположим, что
(3.23)
Равенство (3.21) совместно с ограничениями (3.22)-(3.23) задают на плоскости допустимую область заявок (s1, s2). Поскольку (3.21) монотонна по si, а целевые функции убывают по Сi, то оба партнера будут стремиться снизить заявки si.
Равновесие
Нэша, т.е. равновесие, в котором никому из партнеров не выгодно изменять свою стратегию, при
условии, что остальные не меняют своих стратегий, будет достигнуто в некотором множестве {s1*, s2*}. Если рентабельность i-ro исполнителя рi=(si – Ci)/Ci, то с учетом
равенства (3.21) получим, что p1= p2. Истинные рентабельности 
при этом могут быть и не равны.
Принцип равных прибылей.
Пусть 
С учетом ограничений (3.22)-(3.23) и стремлением исполнителей снизить Сi получим, что множество равновесий Нэша достижимо и при этом прибыли исполнителей будут равны.
Рассмотренные принципы распределения затрат обобщаются на случай любого количества исполнителей и не исчерпывают все варианты [12]. Однако нерешенной остается задача обеспечения неманипулируемости. Покажем, что для любого механизма распределения затрат существует неманипулируемый механизм не меньшей эффективности. Пусть имеется п исполнителей с целевыми функциями:
(3.24)
где qi - доход i-го исполнителя от использования результатов проекта, ji,(Сi) - функция его затрат.
Предположим,
что ji. такие функции, которые имеют единственную точку минимума ri. Доля участия i-го исполнителя
определяется центром на основании заявок s=(s1,..., sn) исполнителей: Ci =pi(s), где функция pi, строго монотонна по si. Величина si также
интерпретируется как мнение i-го исполнителя о справедливом с его точки зрения вкладе в успешную
реализацию проекта. Пусть далее заявки
исполнителей ограничены снизу 
Задача состоит в том, чтобы на основании заявок исполнителей {si} распределить затраты (C1, C2, ..., Сn) так, чтобы С1+С2 +...+ Сп = С, где С- затраты на реализацию проекта.
Проанализируем,
какие заявки будут сообщать исполнители. Пусть s* -равновесные заявки,
тогда, если pi(s*)>ri, то si*=di если sj*>dj, тогда 
Алгоритм нахождения равновесия строится следующим образом.
1. Распределим затраты, считая si* = di,i =1..n. Если у j-го партнера pj(s) < rj, считаем Cj = rj, а величину (rj - pj(s)) распределим между остальными исполнителями.
2. Повторяем п. 1 конечное число раз до тех пор, пока все исполнители не разделятся на два непересекающихся подмножества -- приоритетных, доля которых такова, какую они считают справедливой и остальных, сообщающих в равновесии минимальную заявку.
В
механизме распределения затрат, в котором исполнители сообщают свое мнение 
о справедливом распределении, центр вычисляет
на основании сообщенных оценок s*(
) в соответствии с
приведенным выше алгоритмом. В этом случае сообщение достоверной информации
является равновесием Нэша, то есть механизм является неманипулируемым. Таким
образом, в предположении (3.24) без ограничений (3.22)-(3.23) для любого
механизма распределения затрат найдется неманипулируемый механизм не меньшей
эффективности [9, 67].
Далее рассмотрим модели смешанного финансирования сетевых проектов, которые предполагают, долевое участие центра (фонда развития).
Примем, что имеется п типов проектов, к реализации которых желательно привлечь средства партнеров, входящих в сеть. Однако, проекты могут быть экономически невыгодны для партнеров. Обозначим эффект от проектов на единицу вложенных средств для i-го партнера через ai , где ai <1, i=1…n.
Бюджет центра (фонд развития), как правило, ограничен и недостаточен для реализации необходимого числа проектов. Суть смешанного финансирования состоит в том, что средства выделяются центром при условии, что партнер-исполнитель обязуется выделить на проект и собственное средства. На практике можно фиксировать долю средств, которую должен обеспечить партнер. Фиксация доли средств центра имеет свои минусы. В случае, если эта доля мала, то может быть и незначительный объем привлекаемых от партнеров средств, если велика, то, во-первых, будет слишком много желающих получить средства и возникнет необходимость проведения дополнительных отборов, а во-вторых, уменьшается эффективность использования средств центра.
Далее рассмотрим модель с гибко настраиваемой величиной доли бюджетного финансирования.
Постановка задачи:
Пусть имеются п партнеров (агентов) сети - потенциальных инвесторов в проекты, выгодные как самим агентам, так и виртуальному предприятию в целом. Имеется также централизованный фонд финансирования таких проектов (внутренних заказов). Каждый агент предлагает для реализации проекты, требующие суммарного финансирования Si. Эти проекты проходят экспертизу, в результате которой определяется их общая ценность для виртуального предприятия fi(Si). Помимо общей ценности для предприятия, проекты имеют экономическую ценность ji(Si) для партнера-исполнителя. На основе заявок центр определяет объемы финансирования проектов партнеров {xi}, исходя из ограниченного объема средств центра R. Процедура {xi = p i (S)), i =1..n} является механизмом смешанного финансирования. Оставшиеся средства уi =Si-xi партнер финансирует сам. Прибыль партнера можно описать выражением
(3.25)
Тогда задача заключается в максимизации прибыли центра при механизме финансирования p(S):
где S* = { Si*} - равновесные (по Нэшу) стратегии партнеров.
Рассмотрим линейный случай, когда ji(Si)=aiSi, fi(Si)=biSi, 0<аi<1, bi>0, i=1..n. Используем приоритеты исполнителей при формировании плана финансирования [12], причем в случае прямых приоритетов – xi является возрастающей функцией Si :
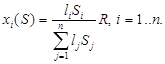(3.26)
В (3.26) li - приоритет i-й фирмы, S= (S1, S2, ..., Sn).
Примем для упрощения без нарушения общности R=1. Из (3.26) следует, что фирма может получить большее финансирование, чем заявлялось Xi(St) > Sh, , тогда остаток Xi(S,)-- St остается у фирмы. Для нахождения равновесия Нэша подставим (3.26) в (3.25)
где 
И максимизирую по Si последнее выражение, получим
где 
Из условия 
находим
и 
(3.27)
где
Должно выполняться условие Si*≥0 или
(3.28)
Партнеры, для которых не выполняется условие (3.28), не финансируются и выбывают из состава претендентов и значения Q и п пересчитываются. За конечное число шагов получим ситуацию равновесия, в которой для всех партнеров выполняется (3.28).
Решая задачу относительно максимизации прибыли центра Ф, необходимо определить приоритеты li (li > 0) таким образом, чтобы суммарный эффект был максимальным:
Выполнив в последнем выражении замену
,
получим:
Определим максимальное значение последнего функционала при
выполнении условия нормирования: 
С помощью метода
множителей
Лагранжа в итоге получим: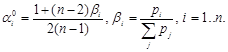 
Тогда
За счет выбора оптимального механизма смешанного финансирования увеличивается суммарная прибыль центра при неизменном объеме затрат центра.
Пусть далее функция эффекта от реализации проектов для i-го исполнителя не линейна и имеет, например, вид:
(3.29)
В этом случае фирма получает прибыль:
Пусть финансирование осуществляется по механизму прямых приоритетов [28], т. е.:
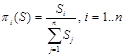
Предположим,
что партнеры не учитывают влияния своей заявки на общие приоритеты (гипотеза
слабого влияния) 
. В этом случае равновесная заявляемая
потребность в финансировании i-ого партнера определяется также как и выше
и получаем
или 
где S определяется из уравнения
(3.30)
Последнее
уравнение всегда имеет единственное решение S* > 1. Причем, если H>1,то 
и всегда имеет место S*>Н.
Следовательно, механизм смешанного финансирования обеспечивает привлечение средств партнеров большее, чем в случае непосредственного финансирования партнерами проектов. При непосредственном финансировании партнер i получает максимум прибыли при объеме финансирования Si — ri поэтому суммарное привлечение средств, в случае прямого финансирования, составит величину Н. Причем, делая замену в (3.30) u=S/H, получим уравнение
анализ которого показывает, что с ростом а растет и и, что означает: эффект от механизма смешанного финансирования тем больше, чем больше параметр a в функциях эффекта партнеров.
| Предыдущая |