А.В. Катаев
Виртуальные бизнес-организации
СПб.: Изд-во Политехнического университета, 2009. – 120 с.
| Предыдущая |
Глава 3. Модели распределения партнеров и заказов в долгосрочных виртуальных предприятиях
3.4. Задачи управления надежностью выполнения заказа
Рассмотрим задачу управления надежностью заказа (проекта). Предположим, что заданы требования заказа - область допустимых результатов (сроки, затраты, качество и др.). Под надежностью выполнения заказа проекта в широком смысле можно понимать свойство сохранения основных параметров внутри допустимой области при возможных воздействиях неблагоприятного характера [10]. В узком смысле под надежностью проекта будем понимать вероятность его успешного завершения в требуемые сроки и с требуемыми параметрами. Двойственным к надежности является понятие риска - вероятность невыполнения проекта, т.е. вероятности того, что результаты проекта окажутся вне допустимой области.
Надежность проекта в целом, зависит от надежности исполнителей. Если требования к результатам проекта заданы и известны характеристики внешних факторов, то центр (организатор) может управлять только надежностью исполнителей. При этом можно выделить управление трех видов.
Во-первых, имея характеристики потенциальных исполнителей (партнеров), центр может выбрать тех из них, которые обеспечат минимальный риск. Эта задача управления надежностью решается на стадии формирования состава исполнителей.
Во-вторых, система управления должна обеспечивать максимальную надежность при фиксированном составе исполнителей. Пусть, например, в проекте участвуют п исполнителей. Пусть известны надежности исполнителей qi, зависящие от выделенного им финансирования Сi:
где ei < 1 - некоторые положительные константы, R - суммарное количество ресурса.
При нулевом финансировании надежность исполнителя равна нулю, при этом риск исполнителя (вероятность невыполнения задания) равен единице. С ростом финансирования надежность возрастает (риск уменьшается). Отметим, что в случае, когда i-й исполнитель получает все финансирование (Ci=R), его риск равен e.
Зная надежность исполнителей, можно определить надежность проекта в целом. Предположим, что проект считается невыполненным, если хотя бы один из исполнителей не выполнил свое задание. Тогда надежность проекта Q в предположении независимости отказов исполнителей равна:
Надежность Q(q1...,qn) зависит от вектора С = (С1,...,Сп) распределения финансирования. Если фонд финансирования ограничен, т.е. имеет место:
то центр может на начальной стадии реализации проекта решить задачу максимизации надежности - максимизировать выбором вектора С надежность при балансовом ограничении. В рассматриваемом примере оптимальным оказывается следующее распределение ресурса:
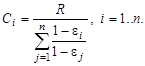
Таким образом, выбор соответствующего распределения финансирования повышает надежность проекта.
Третьим видом управления является оперативное управление надежностью проекта - если в процессе выполнения проекта обнаружена возможность того, что в будущем произойдут какие-то срывы (или они уже произошли), то в ряде случаев можно принять меры и успеть исправить ситуацию, предотвратив срыв проекта в целом.
Можно выделить два подхода к методам повышения надежности любой системы. Если партнеры (исполнители проекта) не являются абсолютно надежными, то есть существуют ненулевые вероятности невыполнения заданий, то для повышения надежности системы следует вводить избыточность, что требует определенных затрат. В этом случае возникает оптимизационная задача заключающаяся в определение оптимального соотношения между надежностью и затратами («риск – эффективность»).
Выделим два типа избыточности – функциональная и компетентностная. Функциональной избыточности соответствует случай, когда в состав исполнителей вводятся дублирующие друг друга исполнители, делающие независимо одинаковую работу. Компетентностной избыточности соответствует введение в состав проекта таких исполнителей, которые обладают дублирующими компетентностями, которые могут потребоваться в случае «отказа» определенных исполнителей. Как правило, использование компетентностной избыточности может заключаться в совместном выполнении несколькими исполнителями одной задачи либо в назначение «куратором» определенной задачи, исполнителя обладающего компетентностью для выполнения задачи в случае «сбоев».
В предположении о независимости исполнителей, риск проекта и оптимальное их число определяются методами теории вероятностей достаточно просто. Если же исполнители взаимозависимы, и надежность проекта сложным образом зависит от надежностей исполнителей, то следует использовать более сложные модели.
Очевидно, что в случае малонадежных исполнителей затраты на выпуск продукции больше, чем при абсолютно надежных исполнителях. Введение такого рода избыточности, помимо дополнительных затрат и повышения надежности, имеет ряд других важных аспектов. Если центр ориентируется, например, на ожидаемый объем выпуска продукции, то он вынужден привлекать большее число исполнителей, чем это минимально необходимо. Так как отказ исполнителя является случайной величиной, то ожидаемый объем выпуска является «усредненным» показателем. На самом деле могут «отказать» все исполнители (тогда центр несет расходы, связанные с невыполнением проекта). Однако, возможна ситуация, когда ни один из исполнителей не откажет. Тогда произведенный объем продукции окажется больше, чем требуемый. Если Центр имеет возможность реализовать этот «излишек», то он получит дополнительную прибыль, в противном случае Центр опять несет расходы. Таким образом, в случае, когда результат проекта зависит от случайных и неопределенных факторов, выбор Центром критериев оптимальности играет существенную роль.
На практике существует следующая проблема: что «лучше» - для выполнения одной и той же работы привлечь одного высокооплачиваемого и высоконадежного исполнителя или большое число (n) менее надежных исполнителей, требующих меньшей оплаты? Предположим, что доход центра от реализации проекта равен R, затраты надежного исполнителя (вероятность отказа – р0) равны С0, а одного ненадежного (с вероятностью отказа r»r0) – С«С0. Сравнивая ожидаемые расходы, получим, что привлечение нескольких ненадежных исполнителей выгоднее, если
Сравнение по ожидаемым потерям с учетом дополнительных затрат может привести к другим условиям.
Основной проблемой при выборе уровня избыточности (числа дублирующих партнеров) является рост затрат. Построение адекватной модели проекта, то есть модели, связывающей риск (надежность) и затраты, позволяет в большинстве случаев достаточно просто определить оптимальный состав исполнителей проекта и оптимальное с точки зрения надежности распределение финансирования между ними.
С одной стороны, введение дублирующих исполнителей является одним из наиболее широко используемых методов повышения надежности. С другой стороны, в ряде случаев простое дублирование исполнителей выглядит не естественно. Увеличение числа взаимозаменяемых исполнителей с одной стороны повышает надежность, а с другой - требует затрат. Задача центра заключается в поиск оптимального соотношения между надежностью и затратами.
Представим проект в виде набора требований F - функций, которые должны реализовывать исполнители к
моменту окончания
проекта, F = (f1,...,fn), где fi - функция, реализуемая i-м исполнителем. Рассмотрим некоторое
множество исполнителей, обладающих набором функций F. Будем
называть набор исполнителей функционально полным (ФП) относительно целей
проекта 
, если любая функция из может реализоваться исполнителями
(одним или их комбинацией). Ясно, что одних и тех же целей можно достичь
различными путями, то есть, в общем случае, существует достаточно много
исполнителей, функционально полных в F. Набор
исполнителей будет минимально полным, если отказ хотя бы одного
из исполнителей приводит к потере функциональной полноты - отказу
проекта в целом. Если одна из функций одного из исполнителей может быть
заменена комбинацией функций других исполнителей, то эта функция
является избыточной, а набор исполнителей - функционально избыточным.
Очевидно, что функционально избыточный набор исполнителей обладает не меньшей надежностью, чем минимально полный. Для решения задачи формирования оптимального состава исполнителей проекта центр должен:
1.
Сформулировать набор требований к проекту .
2.
Из множества потенциальных исполнителей выбрать
функционально полные относительно подмножества.
3. Для каждого из этих подмножеств определить надежность проекта и затраты.
4. Определить оптимальную с той или иной точки зрения комбинацию надежности и затрат, удовлетворяющую дополнительным ограничениям.
При анализе надежности предполагалось, что характеристики исполнителей известны. Информация об этих характеристиках может быть получена либо на основе накопленной информации о деятельности партнера в сети, либо в результате проведения экспертизы, либо от самих исполнителей (самооценка).
| Предыдущая |